Question

已知函数f（x）=

ax2+x，x≥0 x-ax2，x＜0

，设关于x的不等式f（x+a）＜f（x）的解集为M．若[-

1

2

，

1

2

]⊆M，则实数a的取值范围是（　　）

• A、（

  1- 5

  2

  ，0）∪（0，

  1+ 3

  2

  ）
• B、（

  1- 3

  2

  ，0）
• C、（

  1- 5

  2

  ，0）
• D、（-∞，

  1- 5

  2

  ）

Answer 1

考点：分段函数的应用

专题：计算题,函数的性质及应用

分析：首先判断函数f（x）的奇偶性和单调性，可将函数化为f（x）=x+ax|x|，讨论a≥0，由图象平移可得，不等式无解，从而a＜0，再由单调性可得，f（a-

1

2

）＜f（-

1

2

）且f（a+

1

2

）＜f（

1

2

），解出不等式，求其交集即可．

解答： 解：函数f（x）=

ax2+x，x≥0 x-ax2，x＜0

，则f（x）=x+ax|x|，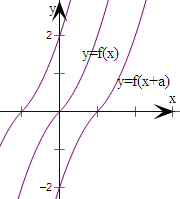
而f（-x）=-x-ax|-x|=-f（x），
则f（x）为奇函数，且为增函数，
若a≥0，将图象向左平移a个单位，
得到f（x+a）的图象，恒在y=f（x）的图象上方，
即f（x+a）＜f（x）不成立；故a＜0．
由于[-

1

2

，

1

2

]⊆M，f（x+a）＜f（x），则f（a-

1

2

）＜f（-

1

2

）且f（a+

1

2

）
＜f（

1

2

），化简得，1+（a-

1

2

）（

1

2

-a）＞-

1

4

且1+（a+

1

2

）|a+

1

2

|＞

1

4

，（a＜0）
由于x|x|＞-

3

4

得到x＞-

3

2

，故有

1- 5

2

＜a＜0且

-1- 3

2

＜a＜0，
所以a的取值范围是（

1- 5

2

，0）．
故选C．

点评：本题考查分段函数的图象和性质，考查函数的单调性和运用，以及图象平移与不等式的关系，考查集合的包含关系，考查数形结合的思想方法，属于中档题．