题目内容
8.已知数列{an}满足:an=n•3n(n∈N*),则此数列前n项和为Sn=$\frac{2n-1}{4}$•3n+1+$\frac{3}{4}$.分析 利用“错位相减法”与等比数列的前n项和公式即可得出.
解答 解:∵an=n•3n,
则此数列的前n项和Sn=3+2×32+3×33+…+n•3n,
∴3Sn=32+2×33+…+(n-1)•3n+n•3n+1,
∴-2Sn=3+32+33+…+3n-n•3n+1=$\frac{3(1-{3}^{n})}{1-3}$-n•3n+1=($\frac{1}{2}$-n)3n+1-$\frac{3}{2}$,
∴Sn=$\frac{2n-1}{4}$•3n+1+$\frac{3}{4}$.
故答案为:$\frac{2n-1}{4}$•3n+1+$\frac{3}{4}$.
点评 本题考查了“错位相减法”与等比数列的前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
18.已知一个扇形的周长是6cm,该扇形的中心角是1弧度,则该扇形的面积为( )cm2.
| A. | 2 | B. | 4 | C. | 6 | D. | 7 |
13.参数方程$\left\{{\begin{array}{l}{x={{cos}^2}θ}\\{y={{sin}^2}θ}\end{array}}\right.$(θ为参数)表示的曲线是( )
| A. | 直线 | B. | 圆 | C. | 线段 | D. | 射线 |
17.已知直线m,n与平面α,β,下列四个命题为真命题的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n⊥α,则m∥n | ||
| C. | 若m∥α,n∥α,β∥α,则m∥n | D. | 若m∥n,m∥α,则n∥α |
18.从全体3位正整数中任取一数,则此数以2为底的对数也是正整数的概率为( )
| A. | $\frac{1}{225}$ | B. | $\frac{1}{300}$ | C. | $\frac{1}{450}$ | D. | 以上全不对 |
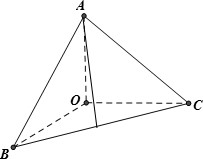 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.