题目内容
20.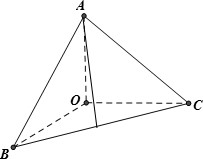 如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
如图所示,在三棱锥A-OBC中,OA,OB,OC两两垂直且长度都为2,则这个三棱锥的体积为$\frac{4}{3}$;O到平面ABC的距离为$\frac{2\sqrt{3}}{3}$.
分析 由OA⊥OB⊥OC,且OA=OB=OC=2,直接利用棱锥体积公式求得三棱锥体积;由已知可得,AB=AC=BC=2$\sqrt{2}$,可得三棱锥O-ABC为正三棱锥,过O作OG⊥平面ABC于G,则G为正三角形的重心,连接AG并延长交BC于D,求得AD,再由重心性质可得AG,最后利用勾股定理求得答案.
解答 解:∵OA⊥OB⊥OC,且OA=OB=OC=2,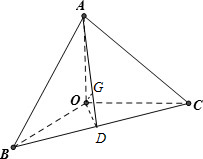
则${V}_{A-OBC}=\frac{1}{3}×\frac{1}{2}×2×2×2=\frac{4}{3}$,
即三棱锥的体积为$\frac{4}{3}$;
由已知可得,AB=AC=BC=2$\sqrt{2}$,
则三棱锥O-ABC为正三棱锥,过O作OG⊥平面ABC于G,则G为正三角形的中心,也是重心,
连接AG并延长交BC于D,则AD⊥BC,
∵AB=2$\sqrt{2}$,BD=$\sqrt{2}$,
∴AD=$\sqrt{(2\sqrt{2})^{2}-(\sqrt{2})^{2}}=\sqrt{6}$,
∴AG=$\frac{2}{3}AD=\frac{2\sqrt{6}}{3}$,
∴OG=$\sqrt{O{A}^{2}-A{G}^{2}}=\sqrt{{2}^{2}-(\frac{2\sqrt{6}}{3})^{2}}=\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{4}{3}$,$\frac{2\sqrt{3}}{3}$.
点评 本题考查棱锥体积的求法,考查了三角形重心的性质,是中档题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
10.函数y=(1+cos2x)•sin2x是( )
| A. | 以π为周期的奇函数 | B. | 以$\frac{π}{2}$为周期的奇函数 | ||
| C. | 以π为周期的偶函数 | D. | 以$\frac{π}{2}$为周期的偶函数 |
15.若a,b,c∈R,且a>b,则下列不等式一定成立的是( )
| A. | a+c>b-c | B. | ac>bc | C. | a2>b2 | D. | (a-b)c2≥0 |
5.已知函数f(x)在定义域(0,+∞)上是单调函数,若对任意x∈(0,+∞),都有f[f(x)-$\frac{1}{x}$]=2,则f($\frac{1}{6}$)的值是( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |