题目内容
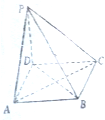 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=| 2 |
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
(3)求证:∠PCD为二面角P-BC-D的平面角.
考点:平面与平面垂直的判定,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)由题意及图形利用线面垂直的判定定理即可得证;
(2)由(1)可得PD⊥AC,又四边形ABCD为正方形,所以AC⊥BD,由线面垂直的判定定理得到AC⊥平面PBD,进一步利用面面垂直的判断证明;
(3)由(1)可得PD⊥BC,又BC⊥CD,由线面垂直的判断得到BC⊥平面PCD,利用线面垂直的性质定理得到所证.
(2)由(1)可得PD⊥AC,又四边形ABCD为正方形,所以AC⊥BD,由线面垂直的判定定理得到AC⊥平面PBD,进一步利用面面垂直的判断证明;
(3)由(1)可得PD⊥BC,又BC⊥CD,由线面垂直的判断得到BC⊥平面PCD,利用线面垂直的性质定理得到所证.
解答:
(1)证明:∵PA=PC=
a,PD=a
∴PD2+AD2=PA2,即PD⊥AD,
又∵PD⊥CD.AD∩CD=D
∴PD⊥平面ABCD;
(2)由(1)可得PD⊥AC,又四边形ABCD为正方形,所以AC⊥BD,
所以 AC⊥平面PBD,
所以平面PAC⊥平面PBD;
(3)由(1)可得PD⊥BC,又BC⊥CD,所以BC⊥平面PCD,
所以BC⊥CD,BC⊥PC,
所以∠PCD为二面角P-BC-D的平面角.
| 2 |
∴PD2+AD2=PA2,即PD⊥AD,
又∵PD⊥CD.AD∩CD=D
∴PD⊥平面ABCD;
(2)由(1)可得PD⊥AC,又四边形ABCD为正方形,所以AC⊥BD,
所以 AC⊥平面PBD,
所以平面PAC⊥平面PBD;
(3)由(1)可得PD⊥BC,又BC⊥CD,所以BC⊥平面PCD,
所以BC⊥CD,BC⊥PC,
所以∠PCD为二面角P-BC-D的平面角.
点评:本题考查了线面垂直的判定定理和性质定理的运用,关键是熟练掌握线面垂直的判定定理和性质定理.

练习册系列答案
相关题目
若椭圆
+
=1的一个焦点和短轴的两端点构成一个正三角形,则该椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知两条不同的直线m,n,两个不同的平面α,β,在下列条件中可以得出α⊥β的是( )
| A、m⊥n,n∥α,n∥β |
| B、m⊥n,α∩β=n,m?α |
| C、m∥n,n⊥β,m?α |
| D、m∥n,m⊥α,n⊥β |
tan(-
)=( )
| 17π |
| 6 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
已知a,b表示直线,α,β表示平面,下列推理正确的是( )
| A、α∩β=a,b?α⇒a∥b |
| B、α∩β=a,a∥b⇒b∥α且b∥β |
| C、a∥β,b∥β,a?α,b?α⇒α∥β |
| D、α∥β,α∩γ=a,β∩γ=b⇒a∥b |
 在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形且∠BAE=90°,AD⊥AE.
在如图所示的几何体中,四边形ABCD为正方形,△ABE为直角三角形且∠BAE=90°,AD⊥AE.