题目内容
已知两条不同的直线m,n,两个不同的平面α,β,在下列条件中可以得出α⊥β的是( )
| A、m⊥n,n∥α,n∥β |
| B、m⊥n,α∩β=n,m?α |
| C、m∥n,n⊥β,m?α |
| D、m∥n,m⊥α,n⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据面面垂直的判定定理解答.
解答:
解:对于选项A,平面α,β可能平行或者相交但是不一定垂直;故A错误;
对于B,m⊥n,α∩β=n,m?α由此无法得到m⊥β,因此α,β不一定垂直;故B错误;
对于C,由m∥n,n⊥β,可得m⊥β,又m?α,所以α⊥β;故C正确;
对于D,由m∥n,m⊥α得到n⊥α,又n⊥β,所以α∥β,得不到α⊥β;故D错误;
故选C.
对于B,m⊥n,α∩β=n,m?α由此无法得到m⊥β,因此α,β不一定垂直;故B错误;
对于C,由m∥n,n⊥β,可得m⊥β,又m?α,所以α⊥β;故C正确;
对于D,由m∥n,m⊥α得到n⊥α,又n⊥β,所以α∥β,得不到α⊥β;故D错误;
故选C.
点评:本题考查了面面垂直的判定,可以首先得到线面垂直,然后利用面面垂直的判定定理判断.

练习册系列答案
相关题目
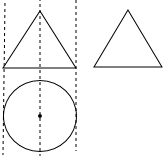 如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )
如图,一个空间几何体的正视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么这个几何体的内切球表面积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
函数f(x)=x-sin2x的图象为( )
A、 |
B、 |
C、 |
D、 |
点P在双曲线C:
-y2=1上,F1、F2是双曲线的焦点,∠F1PF2=60°,则P到x轴的距离为( )
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
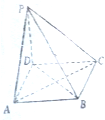 如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面是边长为a的正方形,侧棱PD=a,PA=PC=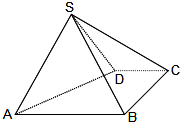 如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=
如图,四棱锥S-ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=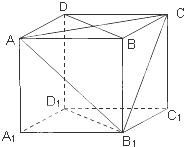 如图,在棱长为1的正方体ABCD-A1B1C1D1中.
如图,在棱长为1的正方体ABCD-A1B1C1D1中.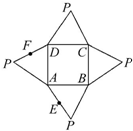 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,在此几何体中,给出下面四个结论: