题目内容
已知点F(0,1),一动圆过点F且与圆x2+(y+1)2=8内切.
(Ⅰ)求动圆圆心的轨迹C的方程;
(Ⅱ)设点A(a,0),点P为曲线C上任一点,求点A到点P距离的最大值d(用a表示).
(Ⅰ)求动圆圆心的轨迹C的方程;
(Ⅱ)设点A(a,0),点P为曲线C上任一点,求点A到点P距离的最大值d(用a表示).
考点:轨迹方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)设圆心坐标为P(x,y),则动圆的半径为r=
,又动圆与x2+(y+1)2=8内切,故
=|2
-r|,由此能求出动圆圆心的轨迹C的方程.
(2)设P(x,y),则|PA|2=(x-a)2+y2=(x-a)2+2-2x2=-(x+a)2+2a2+2,令f(x)=-(x+a)2+2a2+2,x∈[-1,1].再分类讨论能够推导出d(a)=
.
| x2+(y-1)2 |
| x2+(y-1)2 |
| 2 |
(2)设P(x,y),则|PA|2=(x-a)2+y2=(x-a)2+2-2x2=-(x+a)2+2a2+2,令f(x)=-(x+a)2+2a2+2,x∈[-1,1].再分类讨论能够推导出d(a)=
|
解答:
解:(Ⅰ)设圆心坐标为P(x,y),则动圆的半径为r=
,
又动圆与x2+(y+1)2=8内切,
∴
=|2
-r|,
整理得2x2+y2=2,
∴动圆圆心的轨迹C的方程为2x2+y2=2.…(6分)
(Ⅱ)设P(x,y),则
|PA|2=(x-a)2+y2=(x-a)2+2-2x2
=-x2-2ax+a2+2
=-(x+a)2+2a2+2,
令f(x)=-(x+a)2+2a2+2,x∈[-1,1],
∴当-a<-1,即a>1时,f(x)在[-1,1]上是减函数,
[f(x)]max=f(-1)=(a+1)2.
当-1≤-a≤1,即-1≤a≤1时,f(x)在[-1,-a]上是增函数,在[-a,1]上是减函数,
则[f(x)]max=f(-a)=2a2+2.
当-a>1,即a<-1时,f(x)在[-1,1]上是增函数,
[f(x)]max=f(1)=(a-1)2,
∴d(a)=
.…(13分)
| x2+(y-1)2 |
又动圆与x2+(y+1)2=8内切,
∴
| x2+(y-1)2 |
| 2 |
整理得2x2+y2=2,
∴动圆圆心的轨迹C的方程为2x2+y2=2.…(6分)
(Ⅱ)设P(x,y),则
|PA|2=(x-a)2+y2=(x-a)2+2-2x2
=-x2-2ax+a2+2
=-(x+a)2+2a2+2,
令f(x)=-(x+a)2+2a2+2,x∈[-1,1],
∴当-a<-1,即a>1时,f(x)在[-1,1]上是减函数,
[f(x)]max=f(-1)=(a+1)2.
当-1≤-a≤1,即-1≤a≤1时,f(x)在[-1,-a]上是增函数,在[-a,1]上是减函数,
则[f(x)]max=f(-a)=2a2+2.
当-a>1,即a<-1时,f(x)在[-1,1]上是增函数,
[f(x)]max=f(1)=(a-1)2,
∴d(a)=
|
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
数列{an}中,若an+1=
,a1=1,则a2010=( )
| an |
| 2an+1 |
| A、4019 | ||
B、
| ||
| C、4021 | ||
D、
|
 图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )
图是某赛季甲、乙两名篮球运动员每场比赛得分统计的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是( )| A、62 | B、63 | C、64 | D、65 |
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=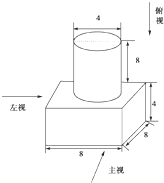 一几何体的直观图如图所示:
一几何体的直观图如图所示: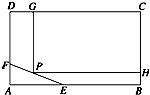 如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.
如图,长方形ABCD形状的空地,AB=100m,BC=80m,现决定在该空地上规划出一块矩形CGPH地面学生公寓,要求一边落在CD 上,但不得越过文物保护区△AEF的EF.△AEF的边AE=30m,AF=20m.