题目内容
已知直线l的参数方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
x+y.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面ρ≤4sin(θ-
)的公共点,求
x+y的取值范围.
|
| 3 |
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面ρ≤4sin(θ-
| π |
| 6 |
| 3 |
考点:参数方程化成普通方程,简单曲线的极坐标方程
专题:计算题,直线与圆,坐标系和参数方程
分析:(1)利用极坐标与直角坐标的方程互化的方法,可得圆C的直角坐标方程;
(2)将
(t为参数),代入z=
x+y得z=-t,又直线l过C(-1,
),圆C的半径是2,可得结论.
(2)将
|
| 3 |
| 3 |
解答:
解:(1)圆C的极坐标方程为ρ=4sin(θ-
),
即有ρ=2
sinθ-2cosθ,
则ρ2=2
ρsinθ-2ρcosθ,即有x2+y2=2
y-2x,
即为圆C:x2+y2+2x-2
y=0;
(2)设z=
x+y,
由圆C的方程x2+y2+2x-2
y=0,可得(x+1)2+(y-
)2=4,
所以圆C的圆心是(-1,
),半径是2,
将
(t为参数),代入z=
x+y得z=-t,
又直线l过C(-1,
),圆C的半径是2,
由题意有:-2≤t≤2,
所以-2≤t≤2.
即
x+y的取值范围是[-2,2].
| π |
| 6 |
即有ρ=2
| 3 |
则ρ2=2
| 3 |
| 3 |
即为圆C:x2+y2+2x-2
| 3 |
(2)设z=
| 3 |
由圆C的方程x2+y2+2x-2
| 3 |
| 3 |
所以圆C的圆心是(-1,
| 3 |
将
|
| 3 |
又直线l过C(-1,
| 3 |
由题意有:-2≤t≤2,
所以-2≤t≤2.
即
| 3 |
点评:本题考查直线的参数方程与圆的极坐标方程与普通方程的互化,直线与圆的位置关系的应用,考查计算能力.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知x、y满足(x-1)2+y2=1,则S=x2+y2+2x-2y+2的最小值是( )
A、6-2
| ||
B、
| ||
C、
| ||
| D、2 |
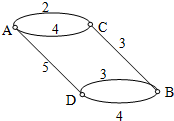 如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )
如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )