题目内容
15.已知f(x)=alnx-x2在区间(0,1)内任取两个不相等的实数p、q,不等式$\frac{f(p)-f(q)}{p-q}>1$恒成立,则实数a的取值范围为( )| A. | (3,5) | B. | (-∞,0) | C. | (3,5] | D. | [3,+∞) |
分析 由不等式进行转化,然后判断函数的单调性,求函数的导数,利用参数分离法进行求解即可.
解答 解:∵p≠q,不妨设p>q,由于$\frac{f(p)-f(q)}{p-q}>1$,
∴f(p)-f(q)>p-q,得[f(p)-p]-[f(q)-q]>0,
∵p>q,∴g(x)=f(x)-x在(0,1)内是增函数,
∴g'(x)>0在(0,1)内恒成立,即$\frac{a}{x}-2x-1$>0恒成立,
a>x(2x+1)的最大值,
∵x∈(0,1)时x(2x+1)<3,
∴实数a的取值范围为[3,+∞).
故选:D.
点评 本题主要考查不等式恒成立问题,根据不等式进行转化判断函数的单调性,分离参数是解决本题的关键,是中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
6.在2016年巴西里约奥运会期间,6名游泳队员从左至右排成一排合影留念,最左边只能排甲或乙,最右端不能排甲,则不同的排法种数为( )
| A. | 216 | B. | 108 | C. | 432 | D. | 120 |
3.下列函数中,既是偶函数又在(0,+∞)上单调递增的是( )
| A. | y=lgx | B. | y=cosx | C. | y=|x| | D. | y=sinx |
10.某研究小组在电脑上进行人工降雨模拟实验,准备用A、B、C三种人工降雨方式分别对甲,乙,丙三地实施人工降雨,其实验统计结果如下
假定对甲、乙、丙三地实施的人工降雨彼此互不影响,且不考虑洪涝灾害,请根据统计数据:
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
| 方式 | 实施地点 | 大雨 | 中雨 | 小雨 | 模拟实验次数 |
| A | 甲 | 2次 | 6次 | 4次 | 12次 |
| B | 乙 | 3次 | 6次 | 3次 | 12次 |
| C | 丙 | 2次 | 2次 | 8次 | 12次 |
(Ⅰ)求甲、乙、丙三地都恰为中雨的概率;
(Ⅱ)考虑不同地区的干旱程度,当雨量达到理想状态时,能缓解旱情,若甲、丙地需中雨即达到理想状态,乙地必须是大雨才达到理想状态,记“甲,乙,丙三地中缓解旱情的个数”为随机变量X,求X的分布列和数学期望.
20.已知i是虚数单位,若z(1+i)=1+3i,则$\overline z$=( )
| A. | 2-i | B. | 2+i | C. | -1+i | D. | -1-i |
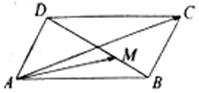 如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.
如图,平行四边形ABCD中,AB=2,AD=1,∠DAB=60°,$\overrightarrow{DM}=2\overrightarrow{MB}$,则$\overrightarrow{AC}•\overrightarrow{AM}$=4.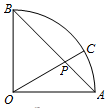 如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.
如图,扇形AOB的圆心角为90°,点P在弦AB上,且OP=$\sqrt{2}$AP,延长OP交弧AB于点C,现向该扇形内随机投一点,则该点落在扇形AOC内的概率为$\frac{1}{3}$.