Question

7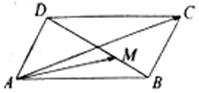．如图，平行四边形ABCD中，AB=2，AD=1，∠DAB=60°，$\overrightarrow{DM}=2\overrightarrow{MB}$，则$\overrightarrow{AC}•\overrightarrow{AM}$=4．

Answer 1

分析 利用平行四边形法和向量的数量积公式计算即可

解答 解：$\overrightarrow{AC}•\overrightarrow{AM}$=（$\overrightarrow{AB}$+$\overrightarrow{AD}$）（$\overrightarrow{AB}$+$\overrightarrow{BM}$），
=（$\overrightarrow{AB}$+$\overrightarrow{AD}$）（$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{BD}$），
=（$\overrightarrow{AB}$+$\overrightarrow{AD}$）[$\overrightarrow{AB}$+$\frac{1}{3}$（$\overrightarrow{AD}$-$\overrightarrow{AB}$）]，
=（$\overrightarrow{AB}$+$\overrightarrow{AD}$）（$\frac{2}{3}$$\overrightarrow{AB}$+$\frac{1}{3}$$\overrightarrow{AD}$），
=$\frac{2}{3}$${\overrightarrow{AB}}^{2}$+$\frac{1}{3}$${\overrightarrow{AD}}^{2}$+$\overrightarrow{AB}$•$\overrightarrow{AD}$，
=$\frac{2}{3}×4$+$\frac{1}{3}$+2×1×$\frac{1}{2}$=4，
故答案为：4

点评 本题考查了平行四边形法则、数量积运算，属于基础题．