题目内容
15．已知含有三个元素的集合A={a，$\frac{b}{a}$，1}，集合B={a2，a+b，0}，若A=B，则b-a=1．分析 根据集合相等定义，两个集合相等，则两个集合中的元素对应相等，又因为分母不能为0，顾很容易可以找到集合中元素之间的对应相等关系，构造方程组，解出a，b值后，代入不难求出b-a的值．
解答 解：若两个集合相等，则集合中元素对应相等，
又因为a为分母，则a≠0，
故$\frac{b}{a}$=0，即b=0；
若a=1，则a2=1，这与集合元素互异性相矛盾，
故a≠1，则a2=1，a=-1．
则b-a=1．
故答案是：1．
点评 解决该类问题的基本方法为：利用集合中元素的特点，列出方程组求解．但解出后应注意检验，看所得结果是否符合元素的互异性．
练习册系列答案
相关题目
15．已知$\frac{{sin2θ+2{{sin}^2}θ}}{1+tanθ}=k（\frac{π}{4}＜θ＜\frac{π}{2}）$，则$sin（θ+\frac{π}{4}）$的值（ ）
| A． | 随着k的增大而增大 | |
| B． | 随着k的增大而减小 | |
| C． | 是一个与k无关的常数 | |
| D． | 有时随k增大而增大，有时随k增大而减小 |
10．
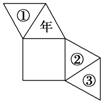某人用如图所示的纸片，沿折痕折后粘成一个四棱锥形的“走马灯”，正方形做灯底，且有一个三角形面上写上了“年”字，当灯旋转时，正好看到“新年快乐”的字样，则在①、②、③处应依次写上（ ）
某人用如图所示的纸片，沿折痕折后粘成一个四棱锥形的“走马灯”，正方形做灯底，且有一个三角形面上写上了“年”字，当灯旋转时，正好看到“新年快乐”的字样，则在①、②、③处应依次写上（ ）| A． | 快、新、乐 | B． | 乐、新、快 | C． | 新、乐、快 | D． | 乐、快、新 |
20．等腰直角三角形AOB内接于抛物线y2=2px（p＞0），O为抛物线的顶点，OA⊥OB，△AOB的面积是16，抛物线的焦点为F，若M是抛物线上的动点，则$\frac{|OM|}{|MF|}$的最大值为（ ）
| A． | $\frac{\sqrt{3}}{3}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\frac{2\sqrt{6}}{3}$ |
7．已知集合A={x|x2-2x＞0}，集合B={x|y=lg（x-1）}，则A∩B=（ ）
| A． | （1，+∞） | B． | （2，+∞） | C． | （-∞，0）∪（2，+∞） | D． | （-∞，0）∪（1，+∞） |
5．从集合{1，2，3，4} 中有放回地随机抽取2次，每次抽取1个数，则2次抽取数之和等于4的概率为（ ）
| A． | $\frac{4}{16}$ | B． | $\frac{3}{16}$ | C． | $\frac{2}{16}$ | D． | $\frac{1}{16}$ |