题目内容
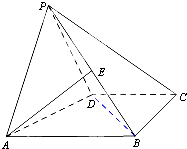 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.(1)求证:PA⊥BD;
(2)若E为侧棱PB的中点,求直线AE与底面ABCD所成角的正弦值.
考点:直线与平面所成的角,直线与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)利用平面ADP⊥平面ABCD,证明BD⊥平面ADP,即可证明PA⊥BD;
(2)证明∠EAH即为直线AE与平面ABCD的所成角,再求出直线AE与底面ABCD所成角的正弦值.
(2)证明∠EAH即为直线AE与平面ABCD的所成角,再求出直线AE与底面ABCD所成角的正弦值.
解答:
 (1)证明:由已知条件易得:AB=4,AD=BD=2
(1)证明:由已知条件易得:AB=4,AD=BD=2
,则BD⊥AD,
又平面ADP⊥平面ABCD,平面ADP∩平面ABCD=AD,BD?平面ABCD,
故BD⊥平面ADP,
又AP?平面ADP,从而有AP⊥BD…(6分)
(2)解:如图,取AD中点O,连接PO,OB,并取OB中点H,连接AH,EH,
∵PA=PD,∴PO⊥AD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
∴PO⊥平面ABCD,
又 EH∥PO,
∴EH⊥平面ABCD
则∠EAH即为直线AE与平面ABCD的所成角
由(1)AP⊥BD,又AP⊥PD,PD∩BD=D∴AP⊥平面PBD∴AP⊥PB,∴PB=
=2
∴AE=
=
∴sin∠EAH=
=
=
,
直线AE与平面ABCD的所成角的正弦值为
.…(14分)
 (1)证明:由已知条件易得:AB=4,AD=BD=2
(1)证明:由已知条件易得:AB=4,AD=BD=2| 2 |
又平面ADP⊥平面ABCD,平面ADP∩平面ABCD=AD,BD?平面ABCD,
故BD⊥平面ADP,
又AP?平面ADP,从而有AP⊥BD…(6分)
(2)解:如图,取AD中点O,连接PO,OB,并取OB中点H,连接AH,EH,
∵PA=PD,∴PO⊥AD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,PO?平面PAD,
∴PO⊥平面ABCD,
又 EH∥PO,
∴EH⊥平面ABCD
则∠EAH即为直线AE与平面ABCD的所成角
由(1)AP⊥BD,又AP⊥PD,PD∩BD=D∴AP⊥平面PBD∴AP⊥PB,∴PB=
| AB2-AP2 |
| 3 |
| AP2+PE2 |
| 7 |
| EH |
| AE |
| ||||
|
| ||
| 14 |
直线AE与平面ABCD的所成角的正弦值为
| ||
| 14 |
点评:本题考查直线AE与底面ABCD所成角的正弦值,考查平面与平面垂直的性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若m.n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是( )
| A、若α∥β,m⊥α,则m⊥β |
| B、若α∩β=m,n与α、β所成的角相等,则m⊥n |
| C、若m∥α,m⊥β,则α⊥β |
| D、若m∥n,m⊥α,则n⊥α |
设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则mn的取值范围是( )
A、[3-2
| ||||
B、(-∞,3-2
| ||||
C、[1-
| ||||
D、(-∞,1-
|
 如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )
如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )| A、GF⊥△DEF所在平面 |
| B、DO⊥△EFG所在平面 |
| C、DG⊥△EFG所在平面 |
| D、GO⊥△EFG所在平面 |
如图是计算t=12×22×…×i2的程序,程序中循环体执行的次数为( )


| A、3 | B、4 | C、5 | D、6 |