题目内容
设m,n∈R,若直线(m+1)x+(n+1)y-2=0与圆(x-1)2+(y-1)2=1相切,则mn的取值范围是( )
A、[3-2
| ||||
B、(-∞,3-2
| ||||
C、[1-
| ||||
D、(-∞,1-
|
考点:直线与圆的位置关系
专题:计算题,直线与圆
分析:由圆的标准方程找出圆心坐标和半径r,由直线与圆相切时,圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关系式,整理后利用基本不等式变形,即可求mn的范围.
解答:
解:由圆的方程(x-1)2+(y-1)2=1,得到圆心坐标为(1,1),半径r=1,
∵直线(m+1)x+(n+1)y-2=0与圆相切,
∴圆心到直线的距离d=
=1,
整理得:m+n+1=mn,
∴(m+n)2=(mn-1)2≥4mn,
设mn=x,则有x2-6x+1≥0,
解得:x≥3+2
或x≤3-2
,
则mn的取值范围为(-∞,3+2
]∪[3+2
,+∞).
故选:B.
∵直线(m+1)x+(n+1)y-2=0与圆相切,
∴圆心到直线的距离d=
| |m+n| | ||
|
整理得:m+n+1=mn,
∴(m+n)2=(mn-1)2≥4mn,
设mn=x,则有x2-6x+1≥0,
解得:x≥3+2
| 2 |
| 2 |
则mn的取值范围为(-∞,3+2
| 2 |
| 2 |
故选:B.
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,基本不等式,以及一元二次不等式的解法,利用了转化及换元的思想,当直线与圆相切时,圆心到直线的距离等于圆的半径,熟练掌握此性质是解本题的关键.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
已知曲线C的方程为x2-xy+y2-2=0,则下列各点中,在曲线C上的点是( )
A、(0,
| ||
| B、(1,-2) | ||
| C、(2,-3) | ||
| D、(3,8) |
 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=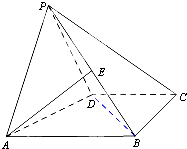 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.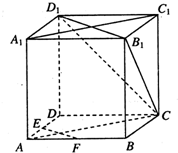 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.