题目内容
若m.n是两条不同的直线,α、β是两个不同的平面,则下列命题不正确的是( )
| A、若α∥β,m⊥α,则m⊥β |
| B、若α∩β=m,n与α、β所成的角相等,则m⊥n |
| C、若m∥α,m⊥β,则α⊥β |
| D、若m∥n,m⊥α,则n⊥α |
考点:命题的真假判断与应用
专题:空间位置关系与距离
分析:A.若α∥β,m⊥α,利用面面平行的性质可判断m⊥β,可判断A;
B.若α∩β=m,则m∥n且n∥α,n∥β时,n与α、β所成的角相等,由此可判断B;
C.若m∥α,m⊥β,不妨令m在平面α内的射影为m′,利用面面垂直的性质可判断α⊥β;
D.若m∥n,m⊥α,利用线线平行的性质可判断D.
B.若α∩β=m,则m∥n且n∥α,n∥β时,n与α、β所成的角相等,由此可判断B;
C.若m∥α,m⊥β,不妨令m在平面α内的射影为m′,利用面面垂直的性质可判断α⊥β;
D.若m∥n,m⊥α,利用线线平行的性质可判断D.
解答:
解:对于A,若α∥β,m⊥α,由面面平行的性质可知,m⊥β,故A正确;
对于B,α∩β=m,若m∥n,且n∥α,n∥β,则n与α、β所成的角相等,故B错误;
对于C,若m∥α,m⊥β,不妨令m在平面α内的射影为m′,则m∥m′,故m′⊥β,由面面垂直的性质定理可知,α⊥β,故C正确;
对于D,若m∥n,m⊥α,由线线平行的性质可知n⊥α,故D正确.
故选:B.
对于B,α∩β=m,若m∥n,且n∥α,n∥β,则n与α、β所成的角相等,故B错误;
对于C,若m∥α,m⊥β,不妨令m在平面α内的射影为m′,则m∥m′,故m′⊥β,由面面垂直的性质定理可知,α⊥β,故C正确;
对于D,若m∥n,m⊥α,由线线平行的性质可知n⊥α,故D正确.
故选:B.
点评:本题考查命题的真假判断与应用,着重考查空间线线、线面及面面的平行与垂直的性质与判定,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若a<b<c,函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-a)(x-c)的零点在区间( )上.
| A、(-∞,a),(a,b) |
| B、(a,b),(b,c) |
| C、(a,c),(c,+∞) |
钱大姐常说“好货不便宜”,她这句话的意思是:“好货”是“不便宜”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=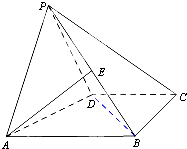 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.