题目内容
已知f(x)=(x-1)ex+1,x∈[0,1]
(Ⅰ)证明:f(x)≥0
(Ⅱ)若a<
<b在x∈(0,1)恒成立,求b-a的最小值.
(Ⅲ)证明:f(x)图象恒在直线y=x-
的上方.
(Ⅰ)证明:f(x)≥0
(Ⅱ)若a<
| ex-1 |
| x |
(Ⅲ)证明:f(x)图象恒在直线y=x-
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)利用导数判断函数的单调性,即可得出f(x)≥f(0)=0;
(Ⅱ)令g(x)=
,利用导数判断函数的单调性,求出函数的最大值、最小值,即可得出a≤1,b≥e-1,即可得出结论;
(Ⅲ)由题意可得只需证f(x)>x-
,即证(x-1)ex-x+
>0在[0,1]上恒成立.令k(x)=(x-1)ex-x+
,利用导数判断函数的单调性,得出最值,即可得出结论.
(Ⅱ)令g(x)=
| ex-1 |
| x |
(Ⅲ)由题意可得只需证f(x)>x-
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
解答:
解:(Ⅰ)f′(x)=xex≥0 即f(x)在[0,1]上单调递增.…(2分)
所以f(x)≥f(0)=0,即结论成立.…(3分)
(Ⅱ)令g(x)=
,则g′(x)=
≥0,x∈(0,1)…(4分)
所以,当x∈(0,1)时,g(x)<g(1)=e-1,
要使
<b,只需b≥e-1 …(5分)
要使
>a成立,只需ex-ax-1>0在x∈(0,1)恒成立.…(6分)
令h(x)=ex-ax-1x∈(0,1)
则h′(x)=ex-a,由x∈(0,1),ex∈(1,e),
当a≤1时,h′(x)≥0 此时x∈(0,1),有h(x)>h(0)=0成立.
所以a≤1满足条件.
当a≥e时,h′(x)≤0,此时x∈(0,1)有h(x)<h(0)=0,
不符合题意,舍去.
当1<a<e时,令h′(x)=0,得x=lna,
可得当x∈(0,lna)时,h′(x)≤0.即x∈(0,lna)时,h(x)<h(0)=0,
不符合题意舍去.
综上,a≤1 …(9分)
又b≥e-1,所以b-a的最小值为e-2.…(10分)
(Ⅲ)由题意只需证f(x)>x-
,即证(x-1)ex-x+
>0在[0,1]上恒成立.
令k(x)=(x-1)ex-x+
,k′(x)=xex-1 …(11分)
k″(x)=(x+1)ex>0,即k′(x)在[0,1]上单调递增.
又k′(
)<0,k′(1)>0,所以k′(x)在[0,1]有唯一的解,记为x0,x0∈(
,1)
且x0ex0-1=0,即ex0=
…(12分)
可得当x∈(0,x0)时,k′(x)≤0,当x∈(x0,1)时,k′(x)≥0,
所以只需最小值k(x0)=(x0-1)ex0-x0+
=
-(x0+
) …(13分)
易得x0+
<
,x0∈(
,1),所以k(x)>0.
所以结论得证.…(14分)
所以f(x)≥f(0)=0,即结论成立.…(3分)
(Ⅱ)令g(x)=
| ex-1 |
| x |
| (x-1)ex+1 |
| x2 |
所以,当x∈(0,1)时,g(x)<g(1)=e-1,
要使
| ex-1 |
| x |
要使
| ex-1 |
| x |
令h(x)=ex-ax-1x∈(0,1)
则h′(x)=ex-a,由x∈(0,1),ex∈(1,e),
当a≤1时,h′(x)≥0 此时x∈(0,1),有h(x)>h(0)=0成立.
所以a≤1满足条件.
当a≥e时,h′(x)≤0,此时x∈(0,1)有h(x)<h(0)=0,
不符合题意,舍去.
当1<a<e时,令h′(x)=0,得x=lna,
可得当x∈(0,lna)时,h′(x)≤0.即x∈(0,lna)时,h(x)<h(0)=0,
不符合题意舍去.
综上,a≤1 …(9分)
又b≥e-1,所以b-a的最小值为e-2.…(10分)
(Ⅲ)由题意只需证f(x)>x-
| 1 |
| 2 |
| 3 |
| 2 |
令k(x)=(x-1)ex-x+
| 3 |
| 2 |
k″(x)=(x+1)ex>0,即k′(x)在[0,1]上单调递增.
又k′(
| 1 |
| 2 |
| 1 |
| 2 |
且x0ex0-1=0,即ex0=
| 1 |
| x0 |
可得当x∈(0,x0)时,k′(x)≤0,当x∈(x0,1)时,k′(x)≥0,
所以只需最小值k(x0)=(x0-1)ex0-x0+
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| x0 |
易得x0+
| 1 |
| x0 |
| 5 |
| 2 |
| 1 |
| 2 |
所以结论得证.…(14分)
点评:本题主要考查利用导数研究函数的有关性质,判断函数的单调性、求函数的极值、最值等知识,考查学生分析问题、解决问题的能力及运算求解能力,属于难题.

练习册系列答案
相关题目
若a<b<c,函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-a)(x-c)的零点在区间( )上.
| A、(-∞,a),(a,b) |
| B、(a,b),(b,c) |
| C、(a,c),(c,+∞) |
钱大姐常说“好货不便宜”,她这句话的意思是:“好货”是“不便宜”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
已知椭圆
+
=1(a>b>0),F为左焦点,A为左顶点,B为上顶点,C为下顶点,且
•
=0,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| CF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=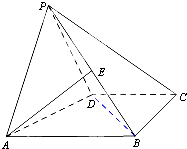 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.