题目内容
已知双曲线C：
-
=1（a＞0，b＞0）的渐近线方程为：y=±
x，右顶点为（1，0）．
（Ⅰ）求双曲线C的方程；
（Ⅱ）已知直线y=x+m与双曲线C交于不同的两点A、B，且线段AB的中点为M（x0，y0）．当x0≠0时，求
的值．
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
（Ⅰ）求双曲线C的方程；
（Ⅱ）已知直线y=x+m与双曲线C交于不同的两点A、B，且线段AB的中点为M（x0，y0）．当x0≠0时，求
| y0 |
| x0 |
考点：直线与圆锥曲线的关系,双曲线的标准方程
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：（Ⅰ）由双曲线的渐近线方程为：y=±
x，得到
=
，又a=1，即可得到双曲线的方程；
（Ⅱ）联立直线方程和双曲线方程，消去y，得到x的方程，再由判别式大于0，运用韦达定理，以及中点坐标公式，得到中点的横坐标，再由直线方程得到纵坐标，进而得到答案．
| b |
| a |
| b |
| a |
| 3 |
（Ⅱ）联立直线方程和双曲线方程，消去y，得到x的方程，再由判别式大于0，运用韦达定理，以及中点坐标公式，得到中点的横坐标，再由直线方程得到纵坐标，进而得到答案．
解答：
解：（Ⅰ）双曲线C：
-
=1（a＞0，b＞0）的渐近线方程为：y=±
x，
则由题意得，
=
，a=1，解得b=
，
则双曲线的方程为：x2-
=1；
（Ⅱ）联立直线方程和双曲线方程，得到，
，消去y，得2x2-2mx-m2-3=0，设A（x1，y1），B（x2，y2），
则判别式△=4m2+8（m2+3）＞0，x1+x2=m，
中点M的x0=
，y0=x0+m=
m，
则有
=3．
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |
则由题意得，
| b |
| a |
| 3 |
| 3 |
则双曲线的方程为：x2-
| y2 |
| 3 |
（Ⅱ）联立直线方程和双曲线方程，得到，
|
则判别式△=4m2+8（m2+3）＞0，x1+x2=m，
中点M的x0=
| m |
| 2 |
| 3 |
| 2 |
则有
| y0 |
| x0 |
点评：本题考查双曲线的方程和性质及运用，考查联立直线方程和双曲线方程，消去未知数，运用韦达定理及中点坐标公式解题，考查运算能力，属于中档题．
练习册系列答案
相关题目
设m，n表示两条不同的直线，α、β表示两个不同的平面，则下列命题中不正确的是（ ）
| A、m⊥α，m⊥β，则α∥β |
| B、m∥n，m⊥α，则n⊥α |
| C、m⊥α，n⊥α，则m∥n |
| D、m∥α，α∩β=n，则m∥n |
钱大姐常说“好货不便宜”，她这句话的意思是：“好货”是“不便宜”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既非充分又非必要条件 |
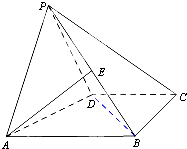如图，在四棱锥P-ABCD中，已知侧面PAD为等腰直角三角形，底面ABCD为直角梯形，AB∥CD，∠ABC=∠APD=90°，侧面PAD⊥底面ABCD，且AB=4，AP=PD=BC=CD=2．
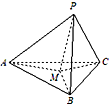如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=2．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（