题目内容
证明：
＜
-
．（n≥2）
| 1 | ||
|
| n |
| n-1 |
考点：不等式的证明
专题：不等式
分析：欲证
＜
-
，只要证
＞
+
．
| 1 | ||
|
| n |
| n-1 |
| n(n+1) |
| n |
| n-1 |
解答：
证明：∵n（n+1）=n（n-1）+2n=[n（n-1）-2
+1]+[n+2
+n-1]
=（
-1]2+（
+
）2＞(
+
)2，
两边开方得：
＞
+
，
∴
＜
=
-
．得证．
| n(n-1) |
| n(n-1) |
=（
| n(n-1) |
| n |
| n-1 |
| n |
| n-1 |
两边开方得：
| n(n+1) |
| n |
| n-1 |
∴
| 1 | ||
|
| 1 | ||||
|
| n |
| n-1 |
点评：本题主要考查不等式的证明，灵活运用不等式的性质进行证明．
练习册系列答案
相关题目
设m，n表示两条不同的直线，α、β表示两个不同的平面，则下列命题中不正确的是（ ）
| A、m⊥α，m⊥β，则α∥β |
| B、m∥n，m⊥α，则n⊥α |
| C、m⊥α，n⊥α，则m∥n |
| D、m∥α，α∩β=n，则m∥n |
若a＜b＜c，函数f（x）=（x-a）（x-b）+（x-b）（x-c）+（x-a）（x-c）的零点在区间（ ）上．
| A、（-∞，a），（a，b） |
| B、（a，b），（b，c） |
| C、（a，c），（c，+∞） |
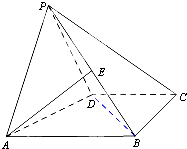如图，在四棱锥P-ABCD中，已知侧面PAD为等腰直角三角形，底面ABCD为直角梯形，AB∥CD，∠ABC=∠APD=90°，侧面PAD⊥底面ABCD，且AB=4，AP=PD=BC=CD=2．