题目内容
 如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )
如图,正方形ABCD中,E,F分别是AB,BC的中点,O是EF的中点,现在沿DE,DF及EF把这个正方形折成一个四面体,使A,B,C三点重合,重合后的点记为G,则在四面体D-EFG中必有( )| A、GF⊥△DEF所在平面 |
| B、DO⊥△EFG所在平面 |
| C、DG⊥△EFG所在平面 |
| D、GO⊥△EFG所在平面 |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:由空间中线线、线面、面面间的位置关系求解.
解答:
解:∵CF与DF不垂直,BF与DF不垂直,
∴GF与DF不垂直,GF与DF不垂直,
∴GF不能垂直于△DEF所在平面,故A错误;
∵DE=DF,O是EF中点,GE=GF,
∴DO⊥EF,GO⊥EF,
∴DO不能垂直于△EFG所在平面,故B错误;
∵DA⊥AE,DC⊥CF,
∴DG⊥GE,DG⊥GF,
∴DG⊥△EFG所在平面,故C正确;
∵GO?△EFG所在平面,
∴GO不可能垂直于△EFG所在平面,故D错误.
故选:C.
∴GF与DF不垂直,GF与DF不垂直,

∴GF不能垂直于△DEF所在平面,故A错误;
∵DE=DF,O是EF中点,GE=GF,
∴DO⊥EF,GO⊥EF,
∴DO不能垂直于△EFG所在平面,故B错误;
∵DA⊥AE,DC⊥CF,
∴DG⊥GE,DG⊥GF,
∴DG⊥△EFG所在平面,故C正确;
∵GO?△EFG所在平面,
∴GO不可能垂直于△EFG所在平面,故D错误.
故选:C.
点评:本题考查命题真假的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
若a<b<c,函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-a)(x-c)的零点在区间( )上.
| A、(-∞,a),(a,b) |
| B、(a,b),(b,c) |
| C、(a,c),(c,+∞) |
已知椭圆
+
=1(a>b>0),F为左焦点,A为左顶点,B为上顶点,C为下顶点,且
•
=0,则椭圆的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| AB |
| CF |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
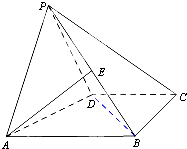 如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.
如图,在四棱锥P-ABCD中,已知侧面PAD为等腰直角三角形,底面ABCD为直角梯形,AB∥CD,∠ABC=∠APD=90°,侧面PAD⊥底面ABCD,且AB=4,AP=PD=BC=CD=2.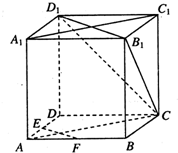 如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别为AD,AB的中点.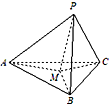 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3,PB=2,PC=2.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(