题目内容
函数f(x)=log0.5(x2-4)的单调增区间为 .
考点:复合函数的单调性
专题:函数的性质及应用
分析:求函数的定义域,根据复合函数单调性之间的关系进行求解即可.
解答:
解:由x2-4>0得x>2或x<-2,
设t=x2-4,则y=log0.5t为减函数,
要求函数f(x)的递增区间,即求函数t=x2-4的递减区间,
∵函数t=x2-4的递减区间为(-∞,-2),
∴函数f(x)=log0.5(x2-4)的单调增区间为(-∞,-2),
故答案为:(-∞,-2)
设t=x2-4,则y=log0.5t为减函数,
要求函数f(x)的递增区间,即求函数t=x2-4的递减区间,
∵函数t=x2-4的递减区间为(-∞,-2),
∴函数f(x)=log0.5(x2-4)的单调增区间为(-∞,-2),
故答案为:(-∞,-2)
点评:本题主要考查函数单调区间的求解,根据复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
已知一组数1,1,2,3,5,8,x,21,34,55,按这组数规律,x应为( )
| A、11 | B、12 | C、13 | D、14 |
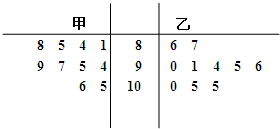 甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分
甲、乙两所学校高三级某学年10次联合考试的理科数学成绩平均分用茎叶图如图所示,则甲乙两所学校的平均分. |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知在?ABCD中,点M在AB上,且AM=3MB,点N在BD上,且
已知在?ABCD中,点M在AB上,且AM=3MB,点N在BD上,且