题目内容
已知函数f(x)=
(a∈R).
(1)若a=3,解不等式f(x)≥2;
(2)若f(x)的定义域为R,求实数a的取值范围.
| |x+1|+|x-a|-2 |
(1)若a=3,解不等式f(x)≥2;
(2)若f(x)的定义域为R,求实数a的取值范围.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)由条件根据绝对值的意义,|x+1|+|x-3|≥6,再根据绝对值的意义求得x的范围.
(2)由题意可得|x+1|+|x-a|≥2恒成立,再根据|x+1|+|x-a|≥|a+1|,可得|1+a|≥2,由此求得a的范围.
(2)由题意可得|x+1|+|x-a|≥2恒成立,再根据|x+1|+|x-a|≥|a+1|,可得|1+a|≥2,由此求得a的范围.
解答:
解:(1)若a=3,f(x)=
,由不等式f(x)≥2,
可得|x+1|+|x-3|-2≥4,∴|x+1|+|x-3|≥6.
而|x+1|+|x-3|表示数轴上的x对应点到-1、3对应点的距离之和,而4和-2对应点到-1、3对应点的距离之和正好等于6,
故由|x+1|+|x-3|≥6可得x≤-2 或x≥4,故原不等式的解集为{x|x≤-2 或x≥4}.
(2)若f(x)的定义域为R,则有|x+1|+|x-a|≥2.
∵|x+1|+|x-a|≥|(x+1)-(x-a)|=|1+a|,∴|1+a|≥2,∴a+1≥2或 a+1≤-2,
由此求得a≥1或a≤-3,故实数a的取值范围为{a|a≥1或a≤-3}.
| |x+1|+|x-3|-2 |
可得|x+1|+|x-3|-2≥4,∴|x+1|+|x-3|≥6.
而|x+1|+|x-3|表示数轴上的x对应点到-1、3对应点的距离之和,而4和-2对应点到-1、3对应点的距离之和正好等于6,
故由|x+1|+|x-3|≥6可得x≤-2 或x≥4,故原不等式的解集为{x|x≤-2 或x≥4}.
(2)若f(x)的定义域为R,则有|x+1|+|x-a|≥2.
∵|x+1|+|x-a|≥|(x+1)-(x-a)|=|1+a|,∴|1+a|≥2,∴a+1≥2或 a+1≤-2,
由此求得a≥1或a≤-3,故实数a的取值范围为{a|a≥1或a≤-3}.
点评:本题主要考查带有绝对值的函数,绝对值的意义、绝对值三角不等式,属于中档题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
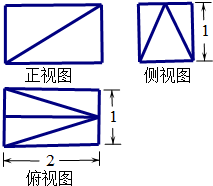
某几何体三视图如图所示,则该几何体的体积为( )

A、
| ||
| B、1 | ||
C、
| ||
D、
|
 已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(x?R,A>0,ω>0,0<φ<