题目内容
12．定圆C：（x-3）2+（y-3）2=（$\frac{5}{2}$）2上有动点P，它关于定点A（7，0）的对称点为Q，点P绕圆心C依逆时针方向旋转120°后到达点R．求线段RQ长度的最大值和最小值．分析 利用圆的参数方程，确定Q，R的坐标，求出QR，即可求线段RQ长度的最大值和最小值．
解答 解：由题意，设P（3+$\frac{5}{2}$cosθ，3+$\frac{5}{2}$sinθ），（θ为参数，0≤θ＜2π），
∵P关于点A（7，0）的对称点为Q，
∴Q（11-$\frac{5}{2}$cosθ，-3-$\frac{5}{2}$sinθ）
∵把点P绕圆心C（3，3）逆时针方向转过120°后得点R，
∴R（3+$\frac{5}{2}$cos（θ+120°），3+$\frac{5}{2}$sin（θ+120°））
∴|QR|2=（$\frac{5}{4}$cosθ-$\frac{5}{4}\sqrt{3}$sinθ-8）2+（$\frac{5}{4}$sinθ+$\frac{5}{4}\sqrt{3}$cosθ+6）2=$\frac{425}{4}$+50sin（θ+α）
∴|QR|的最大值为$\frac{25}{2}$，|QR|的最小值为$\frac{15}{2}$．
点评 本题考查圆的参数方程，考查三角函数知识，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
2．直线l与平面α垂直的一个充分条件是（ ）
| A． | l垂直于平面α内的一条直线 | B． | l垂直于平面α内的两条直线 | ||
| C． | l垂直于平面α内的无数条直线 | D． | l垂直于平面α内的任一条直线 |
3．在区间[0，2]上任取两个实数a、b，则函数f（x）=x2+ax-$\frac{1}{4}$b2+1在区间（-1，1）没有零点的概率为（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{4-π}{4}$ | C． | $\frac{4-π}{8}$ | D． | $\frac{π}{4}$ |
20．已知抛物线C：y2=2px（p＞0），直线l与抛物线C交于A，B两点（不同于原点），以AB为直径的圆过坐标原点O，则关于直线l的判断正确的是（ ）
| A． | 过定点（4p，0） | B． | 过定点（2p，0） | C． | 过定点（p，0） | D． | 过抛物线焦点 |
7．已知函数f（x）=4sin（2x+$\frac{π}{6}$），x∈R，则下列命题正确的是（ ）
| A． | f（x）在区间[0，$\frac{π}{2}$]内是增函数 | |
| B． | 若?x1≠x2，f（x1）=f（x2）=0，则x1-x2必是π的整数倍 | |
| C． | f（x）的图象关于点（-$\frac{π}{12}$+$\frac{kπ}{2}$，0）（k∈Z）对称 | |
| D． | f（x）的图象关于直线x=$\frac{π}{12}$对称 |
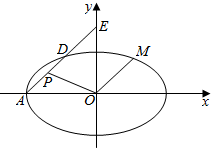如图，在平面直角坐标系xoy中，已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，左顶点为A（-4，0），过点A作斜率为k（k≠0）的直线l交椭圆C于点D，交y轴于点E．