题目内容
3.在区间[0,2]上任取两个实数a、b,则函数f(x)=x2+ax-$\frac{1}{4}$b2+1在区间(-1,1)没有零点的概率为( )| A. | $\frac{π}{8}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{4-π}{8}$ | D. | $\frac{π}{4}$ |
分析 结合一元二次函数的性质求出函数在区间(-1,1)没有零点的等价条件,利用几何概型的概率公式即可得到结论.
解答  解:在区间[0,2]上任取两个数a,b,
解:在区间[0,2]上任取两个数a,b,
则$\left\{\begin{array}{l}{0≤a≤2}\\{0≤b≤2}\end{array}\right.$,对应的平面区域为边长为2的正方形,面积为2×2=4,
∵0≤a≤2,∴抛物线的对称轴为x=-$\frac{a}{2}$∈[-1,0]?[-1,1),
则当x=-$\frac{a}{2}$时,函数取得最小值,
∵0≤b≤2,∴f(0)=1-$\frac{1}{4}$b2∈[0,1],即当0≤x<1上f(x)>0,
∴要使函数f(x)=x2+ax-$\frac{1}{4}$b2+1在区间(-1,1)没有零点,
则函数的最小值$\frac{4×1×(1-\frac{{b}^{2}}{4})-{a}^{2}}{4}$=$\frac{4-{b}^{2}-{a}^{2}}{4}$>0,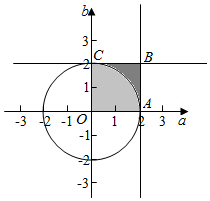
即a2+b2<4,
作出不等式对应的平面区域如图:(阴影部分),
对应的面积S=$\frac{1}{4}×π×{2}^{2}=π$,
则对应的概率P=$\frac{π}{4}$,
故选:D.
点评 本题主要考查几何概型的概率计算,根据函数没有零点的等价条件求出a,b的取值范围是解决本题的关键.利用数形结合和线性规划是解决本题的突破.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.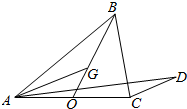 如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )
如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )
 如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )
如图,在△ABC中,BO为边AC上的中线,$\overrightarrow{BG}=2\overrightarrow{GO}$,设$\overrightarrow{CD}$∥$\overrightarrow{AG}$,若$\overrightarrow{AD}=\frac{1}{5}\overrightarrow{AB}+λ\overrightarrow{AC}$(λ∈R),则λ的值为( )| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{6}{5}$ | D. | 2 |
11.在△ABC中,a=7,b=14,A=30°,则此三角形解的情况是( )
| A. | 一解 | B. | 两解 | C. | 一解或两解 | D. | 无解 |