Question

已知集合{（x，y）|

x-3≤0 x+y≥0 x-y≥0

}表示的平面区域为Ω，若在区域Ω内任取一点P（x，y），若点P的坐标满足不等式y≤kx的频率为

2

3

，则k=

 

．

Answer 1

考点：几何概型

专题：概率与统计

分析：由已知画出不等式组求出其对应的面积，即所有基本事件总数对应的几何量，再求出满足x-2y≤0区域的面积，代入几何概型计算公式，即可得到答案．

解答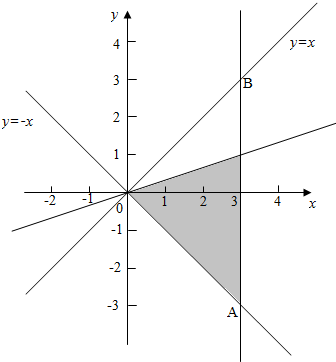： 解：由已知平面区域如图
满足不等式组的区域是三角形OAB，其面积为

1

2

×3×6=9，假设满足不等式y≤kx的区域如图阴影部分，其面积为

1

2

×3×|3k+3|=

3

2

|3k+3|，由几何概型的概率公式得点P的坐标（x，y）满足y≤kx的概率为

2

3

，即

3 2 ×|3k+3|

9

=

2

3

，解得k=

1

3

或者k=-

7

3

＜，由于P在区域Ω内，故-1＜k＜1，所以k=-

7

3

舍去；
故答案为：

1

3

．

点评：本题考查的知识点是几何概型，二元一次不等式（组）与平面区域，求出满足条件A的基本事件对应的“几何度量”（长度、面积、体积），再求出总的基本事件对应的“几何度量”，最后根据概率公式求解．