题目内容
“a≤-1”是“函数f(x)=lnx+ax+
在[1,+∞)上是单调函数”的( )
| 1 |
| x |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:利用导数研究函数的单调性
专题:导数的综合应用,简易逻辑
分析:根据充分条件和必要条件的定义结合函数单调性的性质进行判断即可.
解答:
解:若函数f(x)=lnx+ax+
在[1,+∞)上是单调函数,
则函数的导数f′(x)满足不变号,
即f′(x)≤0或f′(x)≥0在[1,+∞)上恒成立,
∵f′(x)=
+a-
,
∴若函数f(x)单调递减,则f′(x)=
+a-
≤0,即a≤-
+
=(
-
)2-
恒成立,
设g(x)=(
-
)2-
,
∵x≥1,∴0<
≤1,则当
=
时,g(x)取得最小值-
,此时a≤-
,
∴若函数f(x)单调递增,则f′(x)=
+a-
≥0,即a≥-
+
=(
-
)2-
恒成立,
设g(x)=(
-
)2-
,
∵x≥1,∴0<
≤1,
则-
≤g(x)≤0,此时a≥0,
综上若函数f(x)=lnx+ax+
在[1,+∞)上是单调函数,则a≥0或a≤-
,
则“a≤-1”是“函数f(x)=lnx+ax+
在[1,+∞)上是单调函数”的充分不必要条件,
故选:A.
| 1 |
| x |
则函数的导数f′(x)满足不变号,
即f′(x)≤0或f′(x)≥0在[1,+∞)上恒成立,
∵f′(x)=
| 1 |
| x |
| 1 |
| x2 |
∴若函数f(x)单调递减,则f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
设g(x)=(
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
∵x≥1,∴0<
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴若函数f(x)单调递增,则f′(x)=
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
设g(x)=(
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
∵x≥1,∴0<
| 1 |
| x |
则-
| 1 |
| 4 |
综上若函数f(x)=lnx+ax+
| 1 |
| x |
| 1 |
| 4 |
则“a≤-1”是“函数f(x)=lnx+ax+
| 1 |
| x |
故选:A.
点评:本题主要考查充分条件和必要条件的判断以及函数单调性和导数之间的关系,要求熟练掌握导数的应用.

练习册系列答案
相关题目
x2-3x-10>0的解集为( )
| A、(-∞,2)∪(5,+∞) |
| B、(-2,5) |
| C、(-∞,-2)∪(5+∞) |
| D、(-5,2) |
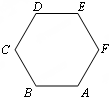
如图,正六边形ABCDEF中,边长为1,|
+
-
|=( )
| BA |
| CD |
| EF |

| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
已知函数f(x)=
若0<x1<x2<1,则( )
| 1-x2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、前三个判断都不正确 |
已知函数f(x)=
,若函数y=f(x+
)+n为奇函数,则实数n等于( )
| 1 |
| 4x+2 |
| 1 |
| 2 |
A、
| ||
| B、0 | ||
C、-
| ||
D、-
|