题目内容
若
+
+
=
，则
，
，
（ ）
| a |
| b |
| c |
| 0 |
| a |
| b |
| c |
| A、一定可以构成三角形 |
| B、都是非零向量时可以构成一个三角形 |
| C、一定不可以构成一个三角形 |
| D、都是非零向量时也可能无法构成三角形 |
考点：向量的加法及其几何意义
专题：平面向量及应用
分析：分类讨论，利用向量的三角形法则、向量共线性质即可得出．
解答：
解：∵
+
+
=
，
则
，
，
都是非零向量且不共线时可以构成一个三角形，而共线时不能构成三角形．
故选：D．
| a |
| b |
| c |
| 0 |
则
| a |
| b |
| c |
故选：D．
点评：本题考查了向量的三角形法则、向量共线性质，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
相关题目
在△ABC中，asinAsinB+bcos2A=2
a，则
=（ ）
| 3 |
| b |
| a |
A、2
| ||
B、2
| ||
C、
| ||
D、
|
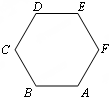
如图，正六边形ABCDEF中，边长为1，|
+
-
|=（ ）
| BA |
| CD |
| EF |
| A、1 | ||
B、
| ||
| C、2 | ||
| D、3 |
复数z满足（z+i）•i=1+i（i是虚数单位），则复数z的模为（ ）
| A、1 | ||
B、
| ||
C、
| ||
| D、3 |