题目内容
7.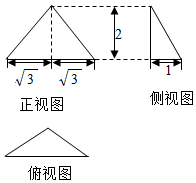 已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )
已知一个三棱锥的三视图如下图所示,其中俯视图是顶角为$\frac{2π}{3}$的等腰三角形,则该三棱锥外接球的表面积为( )| A. | 20π | B. | 16π | C. | 8π | D. | 17π |
分析 作出几何体的三视图,建立空间坐标系,求出外接球的球心,从而得出半径,再计算面积.
解答 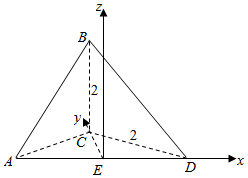 解:作出几何体的直观图如图所示:
解:作出几何体的直观图如图所示:
由三视图可知底面ACD是等腰三角形,∠ACD=$\frac{2π}{3}$,AD=2$\sqrt{3}$,
BC⊥平面ACD,BC=2,
取AD的中点E,连接CE,则CE⊥AD,
以E为原点,以AD为x轴,以EC为y轴,以平面ACD的垂线为z轴建立空间直角坐标系E-xyz,
则A(-$\sqrt{3}$,0,0),B(0,1,2),C(0,1,0),D($\sqrt{3}$,0,0),
设三棱锥的外接球的球心为M(x,y,z),则MA=MB=MC=MD.
∴(x+$\sqrt{3}$)2+y2+z2=x2+(y-1)2+(z-2)2=x2+(y-1)2+z2=(x-$\sqrt{3}$)2+y2+z2,
解得x=0,y=-1,z=1.
∴外接圆的半径r=MA=$\sqrt{3+1+1}$=$\sqrt{5}$.
∴外接球的表面积S=4πr2=20π.
故选:A.
点评 本题考查了棱锥的三视图,球与棱锥的位置关系,属于中档题.

练习册系列答案
相关题目
17.已知a,b∈R,ab>0,则下列不等式中不正确的是( )
| A. | |a+b|≥a-b | B. | $2\sqrt{ab}≤|{a+b}|$ | C. | |a+b|<|a|+|b| | D. | $|{\frac{b}{a}+\frac{a}{b}}|≥2$ |
18.某程序框图如图所示,当输入x的值是1时,输出y的值是( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
15.某程序框图如图所示,该程序运行后输出的值为4,则t的值不可能是( )


| A. | 3 | B. | 6 | C. | 8 | D. | 11 |
2.某几何体的三视图如图所示,则该几何体的外接球的表面积为( )
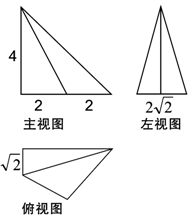

| A. | 136π | B. | 144π | C. | 36π | D. | 34π |
12.下列命题中的真命题是( )
| A. | ?x∈R使得sinx+cosx=1.5 | B. | ?x∈(0,π),sinx>cosx | ||
| C. | ?x∈R使得x2+x=-1 | D. | ?x∈(0,+∞),ex>x+1 |
16.过点(1,1)且与曲线y=x3相切的切线方程为( )
| A. | y=3x-2 | B. | y=$\frac{3}{4}$x+$\frac{1}{4}$ | ||
| C. | y=3x-2或y=$\frac{3}{4}$x+$\frac{1}{4}$ | D. | y=3x-2或y=$\frac{3}{4}$x-$\frac{1}{4}$ |