题目内容
6.设x∈R,向量$\overrightarrow a=(x,1)$,$\overrightarrow b=(1,-2)$,且$\overrightarrow a⊥\overrightarrow b$,则$\overrightarrow a$在$\overrightarrow a+\overrightarrow b$上的投影为$\frac{\sqrt{10}}{2}$.分析 利用向量垂直求出x,然后利用向量的数量积求解$\overrightarrow a$在$\overrightarrow a+\overrightarrow b$上的投影.
解答 截:向量$\overrightarrow a=(x,1)$,$\overrightarrow b=(1,-2)$,且$\overrightarrow a⊥\overrightarrow b$,
可得x-2=0,解得x=2,∴$\overrightarrow{a}$=(2,1).
$\overrightarrow a+\overrightarrow b$=(3,-1).
则$\overrightarrow a$在$\overrightarrow a+\overrightarrow b$上的投影为:$\frac{\overrightarrow{a}•(\overrightarrow{a}+\overrightarrow{b})}{|\overrightarrow{a}+\overrightarrow{b}|}$=$\frac{6-1}{\sqrt{9+1}}$=$\frac{\sqrt{10}}{2}$.
故答案为:$\frac{{\sqrt{10}}}{2}$.
点评 本题考查平面向量的数量积的应用,考查计算能力.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
16.过点(1,1)且与曲线y=x3相切的切线方程为( )
| A. | y=3x-2 | B. | y=$\frac{3}{4}$x+$\frac{1}{4}$ | ||
| C. | y=3x-2或y=$\frac{3}{4}$x+$\frac{1}{4}$ | D. | y=3x-2或y=$\frac{3}{4}$x-$\frac{1}{4}$ |
14.设函数$f(x)=\frac{f'(1)}{e}•{e^x}-f(0)x+\frac{1}{2}{x^2}$,则曲线f(x)在点(1,f(1))处切线方程为( )
| A. | $y=\frac{1}{e}x-\frac{1}{2}$ | B. | $y=ex-\frac{1}{2}$ | C. | $y=-\frac{1}{e}x+\frac{1}{2}$ | D. | $y=ex+\frac{1}{2}$ |
1.已知变量x,y的一组观测数据如表所示:
据此得到的回归方程为$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,若$\stackrel{∧}{a}$=7.9,则x每增加1个单位,y的预测值就( )
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4.0 | 2.5 | -0.5 | 0.5 | -2.0 |
| A. | 增加1.4个单位 | B. | 减少1.4个单位 | C. | 增加1.2个单位 | D. | 减少1.2个单位 |
11.设a=2,b=lg9,c=2sin$\frac{9π}{5}$,则a,b,c的大小关系为( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | c>a>b |
18.已知点F是双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点,过F点作双曲线的一条渐近线垂线,垂足为A,交另一条渐近线于B,若A点恰好为BF的中点,则双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
15.如图所示,某空间几何体的正视图与侧视图相同,则此几何体的表面积为( )
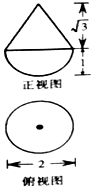

| A. | 6π | B. | $\frac{2π}{3}+\sqrt{3}$ | C. | 4π | D. | $2π+\sqrt{3}$ |
16.如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体的体积为( )


| A. | 32+8π | B. | 32+$\frac{8π}{3}$ | C. | 16+$\frac{8π}{3}$ | D. | 16+8π |