题目内容
已知函数f(x)=x|x-4|,x∈[0,m],其中m∈R且m>0.如果函数f(x)的值域为[0,λm2],试求实数λ的最小值.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:去掉绝对值,画出函数f(x)的图象,结合图象,讨论m的取值,用m表示出λ,根据m的取值,从而求得λ在每种情况下的最小值,对每种情况下的λ作比较,取最小的即可.
解答:
解:∵f(x)=x|x-4|=
;
该函数图象如下:
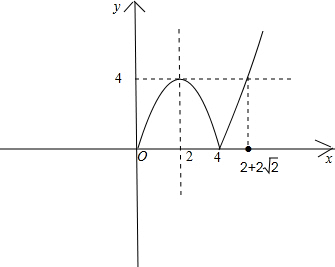
当0<m≤2时,-m2+4m=λm2,解得λ=
-1,
∵0<m≤2,∴
≥
,
-1≥1,∴此时λ最小值为1;
当2<m≤2+2
时,λm2=4,λ=
,
∵2<m≤2+2
,∴4<m2≤12+8
,
≥
=3-2
,
∴此时λ最小值为3-2
;
当m≥2+2
时,m2-4m=λm2,解得λ=1-
,
∵m≥2+2
,∴0<
≤2
-2,
∴1-
≥3-2
,∴此时λ最小值为3-2
;
综上得λ的最小值为3-2
.
|
该函数图象如下:
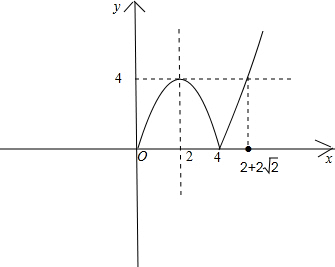
当0<m≤2时,-m2+4m=λm2,解得λ=
| 4 |
| m |
∵0<m≤2,∴
| 1 |
| m |
| 1 |
| 2 |
| 4 |
| m |
当2<m≤2+2
| 2 |
| 4 |
| m2 |
∵2<m≤2+2
| 2 |
| 2 |
| 4 |
| m2 |
| 1 | ||
3+2
|
| 2 |
∴此时λ最小值为3-2
| 2 |
当m≥2+2
| 2 |
| 4 |
| m |
∵m≥2+2
| 2 |
| 4 |
| m |
| 2 |
∴1-
| 4 |
| m |
| 2 |
| 2 |
综上得λ的最小值为3-2
| 2 |
点评:本题考查处理绝对值函数的方法,利用分段函数图象解决问题的方法,以及二次函数图象及值域,根据λ的范围求λ最小值的方法.

练习册系列答案
相关题目
已知(1-x-x8)=a0+a1x+a2x2+…+a21x22,则a1+a2+…+an的值为( )
| A、-1 | B、1 | C、0 | D、-2 |
设x+3y=2,则函数z=3x+27y的最小值是( )
| A、12 | B、27 | C、6 | D、30 |
已知i是虚数单位,集合M=N(整数集),集合N=(i,i2,i3,i4),则集合M∩N的元素共有( )
| A、3个 | B、2个 | C、1个 | D、无穷个 |
 如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.
如图,在海岸线l一侧C处有一个美丽的小岛,某旅游公司为方便游客,在l上设立了A、B两个报名点,满足A、B、C中任意两点间的距离为10千米.公司拟按以下思路运作:先将A、B两处游客分别乘车集中到AB之间的中转点D处(点D异于A、B两点),然后乘同一艘游轮前往C岛.据统计,每批游客A处需发车2辆,B处需发车4辆,每辆汽车每千米耗费2元,游轮每千米耗费12元.设∠CDA=α,每批游客从各自报名点到C岛所需运输成本为S元.