Question

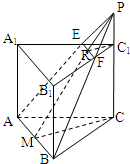已知正三棱柱ABC-A₁B₁C₁底面边长是10，高是12，过底面一边AB，作与底面ABC成60°角的截面面积是

 

．

Answer 1

考点：二面角的平面角及求法

专题：计算题,空间位置关系与距离,空间角

分析：先确定正三棱柱被平面α截得的截面的形状，再计算其面积．

解答： 解：设α与侧棱交于P，取AB的中点M，连接PM，根据题意可知∠PMC=60
∵正三棱柱ABC-A₁B₁C₁的底面边长为10
∴CM=5

3

∵∠PMC=60°
∴PC=15
∵高是12，
∴截面为梯形
∴上底长为（15-12）tan30°×

2

3

=2，下底长为10，高为

12

sin60°

=8

3

，
∴截面的面积是

1

2

•(2+10)•8

3

=48

3

．
故答案为：48

3

．

点评：本题考查正三棱柱被平面α截得的截面面积的计算，确定截面的形状是关键．