Question

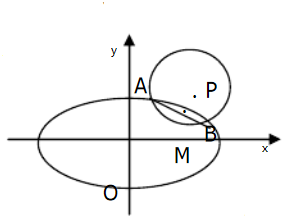
已知以P（2，2）为圆心的圆与椭圆x²+2y²=m交于A、B两点，求弦AB的中点M的轨迹方程．

Answer 1

考点：轨迹方程

专题：计算题,作图题,圆锥曲线的定义、性质与方程

分析：设M（x，y）；A（x₁，y₁），B（x₂，y₂），则由中点坐标公式可得x₁+x₂=2x；y₁+y₂=2y；再由

x

2 1

+2

y

2 1

=m；

x

2 2

+2

y

2 2

=m可化简得

y1-y2

x1-x2

=-

1

2

x1+x2

y1+y2

=-

1

2

x

y

，从而利用直线PM与直线AB垂直求点M的轨迹方程．

解答： 解：设M（x，y）；A（x₁，y₁），B（x₂，y₂）；
则x₁+x₂=2x；y₁+y₂=2y；
由

x

2 1

+2

y

2 1

=m；

x

2 2

+2

y

2 2

=m；
两式相关并同除以（x₁-x₂）得，

y1-y2

x1-x2

=-

1

2

•

x1+x2

y1+y2

=-

1

2

x

y

；
而k_AB=

y1-y2

x1-x2

，k_PM=

y-2

x-2

；
故

y1-y2

x1-x2

•

y-2

x-2

=-1；
即-

1

2

x

y

•

y-2

x-2

=-1；
化简可得点M的轨迹方程为xy+2x-4y=0．

点评：本题考查了圆及椭圆的应用及轨迹方程的求法，属于中档题．