题目内容
已知点F(-
,0),直线n:x=
,动点P到点F的距离等于它到直线l的距离.
(Ⅰ)试判断动点P的轨迹C的形状,并求出其标准方程;
(Ⅱ)若过A(0,2)的直线n与轨迹C有且只有一个公共点,求直线n的方程.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅰ)试判断动点P的轨迹C的形状,并求出其标准方程;
(Ⅱ)若过A(0,2)的直线n与轨迹C有且只有一个公共点,求直线n的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(I)利用抛物线的定义即可得出;
(II)对直线n的斜率分类讨论,当直线l的斜率存在且不为0时,把直线l的方程与抛物线的联立,利用△=0解出即可.
(II)对直线n的斜率分类讨论,当直线l的斜率存在且不为0时,把直线l的方程与抛物线的联立,利用△=0解出即可.
解答:
解:(I)由已知得动点P的轨迹为以点F(
,0)为焦点,以直线l:x=
为准线的抛物线,
∴点P的轨迹方程是y2=-2x.
(II)①当直线n的斜率不存在时,直线n的方程为x=0,直线l与抛物线y2=-2x切于点(0,0).
②当直线n斜率存在时,设直线n的斜率为k,直线n方程为y=kx+2,
代入y2=-2x得:k2x2+2(2k+1)x+4=0.
当k=0时,直线n的方程为y=2,n的方程与抛物线y2=-2x有且只有一个公共点(-2,2).
当k≠0时,由△=0得k=-
,则直线n的方程:x+4y-8=0.
综上所述:所求直线n的方程为x=0和y=2及x+4y-8=0.
| 1 |
| 2 |
| 1 |
| 2 |
∴点P的轨迹方程是y2=-2x.
(II)①当直线n的斜率不存在时,直线n的方程为x=0,直线l与抛物线y2=-2x切于点(0,0).
②当直线n斜率存在时,设直线n的斜率为k,直线n方程为y=kx+2,
代入y2=-2x得:k2x2+2(2k+1)x+4=0.
当k=0时,直线n的方程为y=2,n的方程与抛物线y2=-2x有且只有一个公共点(-2,2).
当k≠0时,由△=0得k=-
| 1 |
| 4 |
综上所述:所求直线n的方程为x=0和y=2及x+4y-8=0.
点评:本题考查了抛物线的定义标准方程、直线与抛物线方程联立转化为方程联立与判别式的关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
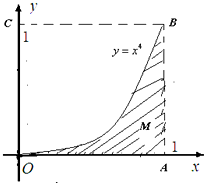 Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分