题目内容
已知函数f(x)=x2-2ax+2,x∈[-4,6]
(1)当a=-1时,求函数的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数.
(1)当a=-1时,求函数的最大值和最小值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:函数的性质及应用
分析:(1)当a=-1时,由题意利用二次函数的性质求得函数的最大值和最小值.
(2)由条件利用二次函数的性质求得实数a的取值范围.
(2)由条件利用二次函数的性质求得实数a的取值范围.
解答:
解:(1)当a=-1时,f(x)=x2+2x+2=(x+1)2+1,x∈[-4,6],
故当x=-1时,函数取得最小值为1,当x=6时,函数取得最大值为50.
(2)由于函数的图象的对称轴方程为x=a,要使y=f(x)在区间[-4,6]上是单调函数,
则有a≤-4,或a≥6,
故当a≤-4,或a≥6时,y=f(x)在区间[-4,6]上是单调函数.
故当x=-1时,函数取得最小值为1,当x=6时,函数取得最大值为50.
(2)由于函数的图象的对称轴方程为x=a,要使y=f(x)在区间[-4,6]上是单调函数,
则有a≤-4,或a≥6,
故当a≤-4,或a≥6时,y=f(x)在区间[-4,6]上是单调函数.
点评:本题主要考查求二次函数在闭区间上的最值,二次函数的性质的应用,属于基础题.

练习册系列答案
相关题目
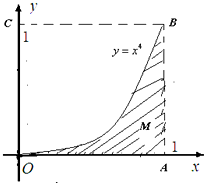 Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分
Monte-Carlo方法在解决数学问题中有广泛的应用.下面是利用Monte-Carlo方法来计算定积分.考虑定积分