题目内容
10.函数y=log2$\frac{1-x}{1+x}$+2,若f(m)=4,则f(-m)=0.分析 由题意可得:log2$\frac{1-m}{1+m}$+2=4,计算可得m的值,由f(-m)=f($\frac{3}{5}$)即可求值得解.
解答 解:由题意可得:log2$\frac{1-m}{1+m}$+2=4,
解得:$\frac{1-m}{1+m}$=4,可得:m=-$\frac{3}{5}$,
故:f(-m)=f($\frac{3}{5}$)=log2$\frac{1-\frac{3}{5}}{1+\frac{3}{5}}$+2=log2$\frac{1}{4}$+2=0.
故答案为:0.
点评 本题主要考查了对数的运算法则的应用,考查了计算能力,属于基础题.

练习册系列答案
相关题目
15.复数z=a+(a+$\frac{1}{a}$)i(a∈R),下列描述中,不正确的是( )
| A. | z不可能是实数 | B. | z不可能是纯虚数 | C. | Rez•Imz≥0 | D. | Imz≥2 |
3.若先将函数y=sin(4x+$\frac{π}{6}$)图象上各点的纵坐标不变,横坐标伸长到原来的2倍,再将所得图象向左平移$\frac{π}{6}$个单位,则所得函数图象的一条对称轴的方程是( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{π}{2}$ |
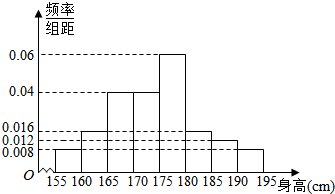 从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.
从某校高二年级800名学生中随机抽取100名测量身高,得到频率分布直方图如图.