题目内容

18．函数y=$\sqrt{x-2}$-$\frac{1}{x+2}$的最小值是-$\frac{1}{4}$．

分析 先确定函数的定义域，再确定函数的单调性，从而求最值．

解答 解：易知函数y=$\sqrt{x-2}$-$\frac{1}{x+2}$的定义域为[2，+∞），
而y=$\sqrt{x-2}$在[2，+∞）上是增函数，
y=$\frac{1}{x+2}$在[2，+∞）上是减函数，
故函数y=$\sqrt{x-2}$-$\frac{1}{x+2}$在在[2，+∞）上是增函数，
故当x=2时，函数有最小值为0-$\frac{1}{4}$=-$\frac{1}{4}$，
故答案为：-$\frac{1}{4}$．

点评 本题考查了函数的定义域的求法及单调性的判断与应用．

练习册系列答案
相关题目
8．设椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$（a＞b＞0）的左、右焦点分别为F1，F2，以F1为圆心，短半轴长为半径的圆与y轴相切，且与直线x-$\sqrt{3}$y-2=0相切．
（1）求椭圆的标准方程；
（2）已知点P（$\sqrt{6}$，0），直线l与椭圆交于A、B两点，且满足$\overrightarrow{PA}$•$\overrightarrow{PB}$=-2，试问直线l是否恒过定点，若恒过定点，请给出证明，并求出该定点的坐标；若不过，请说明理由．
9．若关于x的方程sinx+$\sqrt{3}$cosx+a=0在[0，2π]上有三个实根，则a的值为-$\sqrt{3}$．
6．已知函数f（x）=$\sqrt{{x}^{2}-2ax+3a+2}$在[1，+∞）上是增函数，则a的取值范围是[-3，1]．
13．数列{an}满足a1=$\frac{π}{6}$，an+1∈（-$\frac{π}{2}$，$\frac{π}{2}$），且tanan+1=$\frac{1}{cos{a}_{n}}$（n∈N•），令bn=tan2an，则数列{bn}的前6项和为17．
3．求函数y=sin2（$\frac{π}{12}$-x）+cos2（$\frac{π}{12}$+x）的单调递增区间．
10．函数y=log2$\frac{1-x}{1+x}$+2，若f（m）=4，则f（-m）=0．
7．求过点（2，1），且平行于直线3x-y+5=0的直线方程．
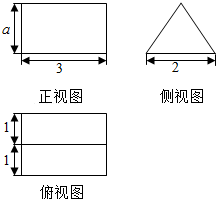11．如图是一个几何体的三视图，若它的体积是3$\sqrt{3}$，则a=$\sqrt{3}$，该几何体的表面积为2$\sqrt{3}$+18．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网