题目内容
已知无穷数列{an}中,a1,a2,…,am是首项为2,公差为3的等差数列;am+1,am+2,…,a2m是首项为2,公比为2的等比数列(其中m≥3,m∈N*),并对任意的n∈N*,均有an+2m=an成立.
(1)当m=14时,求a1000;
(2)若a52=128,试求m的值.
(3)求满足条件an=128的所有n的值(用m表示).
(1)当m=14时,求a1000;
(2)若a52=128,试求m的值.
(3)求满足条件an=128的所有n的值(用m表示).
考点:数列的应用,数列递推式
专题:综合题,等差数列与等比数列
分析:(1)当m=1时,数列的周期为28,于是a1000=a20,依题意可求得a1000;
(2)设am+k是第一个周期中等比数列中的第k项,则am+k=2k,于是128=27,即m≥7,则一个周期中至少有14项,a52最多是第三个周期中的项.对a52是第一个周期中的项、第二个周期中的项、第三个周期中的项,分别讨论计算即可求得m的值;
(3)由an=3n-1=128,得n=43,由am+n=128,n=7,分类讨论,即可求满足条件an=128的所有n的值
(2)设am+k是第一个周期中等比数列中的第k项,则am+k=2k,于是128=27,即m≥7,则一个周期中至少有14项,a52最多是第三个周期中的项.对a52是第一个周期中的项、第二个周期中的项、第三个周期中的项,分别讨论计算即可求得m的值;
(3)由an=3n-1=128,得n=43,由am+n=128,n=7,分类讨论,即可求满足条件an=128的所有n的值
解答:
解:由题设得:an=3n-1,(1≤n≤m),am+n=2n(1≤n≤m),------------(2分)
(1)m=14时,数列的周期为28.
∵1000=28×35+20,而a20是等比数列中的项,
∴a1000=a20=a14+6=26=64.--------------------------------------------------(4分)
(2)显然,a52=128不是数列{an}中等差数列的项.
设am+k是第一个周期中等比数列中的第k项,则am+k=2k.
∵128=27,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
∴a52最多是第三个周期中的项.
若a52是第一个周期中的项,则a52=am+7=128.
∴m=52-7=45;---------------(6分)
若a52是第二个周期中的项,则a52=a3m+7=128.∴3m=45,m=15;---------------(8分)
若a52是第三个周期中的项,则a52=a5m+7=128.∴5m=45,m=9;
综上,m=45,或15,或9.----------------------(10分)
(3)由an=3n-1=128,得n=43,由am+n=128,n=7.
当1≤m≤6时,不存在n使an=128,-------------------------(12分)
当7≤m≤42时,数列中成等差数列的项中不存在128的项,等比数列中,am+7=128.
∴满足条件的n=(2k+1)m+7,k∈N.------------------------------(14分)
当m≥43时,第一周期中,a43=128,am+7=128,
∴满足条件的n=43+2km,或n=(2k+1)m+7,k∈N.------------(16分)
(1)m=14时,数列的周期为28.
∵1000=28×35+20,而a20是等比数列中的项,
∴a1000=a20=a14+6=26=64.--------------------------------------------------(4分)
(2)显然,a52=128不是数列{an}中等差数列的项.
设am+k是第一个周期中等比数列中的第k项,则am+k=2k.
∵128=27,∴等比数列中至少有7项,即m≥7,则一个周期中至少有14项.
∴a52最多是第三个周期中的项.
若a52是第一个周期中的项,则a52=am+7=128.
∴m=52-7=45;---------------(6分)
若a52是第二个周期中的项,则a52=a3m+7=128.∴3m=45,m=15;---------------(8分)
若a52是第三个周期中的项,则a52=a5m+7=128.∴5m=45,m=9;
综上,m=45,或15,或9.----------------------(10分)
(3)由an=3n-1=128,得n=43,由am+n=128,n=7.
当1≤m≤6时,不存在n使an=128,-------------------------(12分)
当7≤m≤42时,数列中成等差数列的项中不存在128的项,等比数列中,am+7=128.
∴满足条件的n=(2k+1)m+7,k∈N.------------------------------(14分)
当m≥43时,第一周期中,a43=128,am+7=128,
∴满足条件的n=43+2km,或n=(2k+1)m+7,k∈N.------------(16分)
点评:本题考查数列的求和,着重考查数列的函数特性,考查其周期性、单调性与最值,突出分类讨论思想与等价转化思想的综合应用,属于难题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
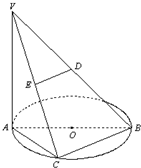 如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.
如图,AB是圆O的直径,点C是弧AB的中点,D,E分别是VB,VC的中点,VA⊥平面ABC.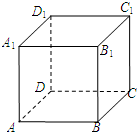 在如图所示的正方体ABCD-A1B1C1D1中,E、F分别为棱AB与AA1的中点,则直线EF与平面ACC1A1成角的大小为
在如图所示的正方体ABCD-A1B1C1D1中,E、F分别为棱AB与AA1的中点,则直线EF与平面ACC1A1成角的大小为