题目内容
已知向量
=(2,0),向量
与向量
-
的夹角为
,则|
|的最大值为 .
| a |
| b |
| b |
| a |
| π |
| 6 |
| b |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,设
=
,
=
,可得
=
+
.设
-
=
,
=
+
.在△OBC中,由正弦定理可得
=
,再利用正弦函数的单调性即可得出.
| OA |
| a |
| OC |
| c |
| OB |
| a |
| c |
| b |
| a |
| c |
| b |
| a |
| c |
|
| ||
| sin∠COB |
|
| ||
| sin∠OCB |
解答:
解:如图所示,
设
=
,
=
,
则
=
+
.
设
-
=
,则
=
+
.
∴∠COB=
.
在△OBC中,由正弦定理可得
=
,
∴|
|=
•sin∠OCB≤4,当且仅当∠OCB=
时取等号,
因此|
|的最大值为4.
故答案为:4.

设
| OA |
| a |
| OC |
| c |
则
| OB |
| a |
| c |
设
| b |
| a |
| c |
| b |
| a |
| c |
∴∠COB=
| π |
| 6 |
在△OBC中,由正弦定理可得
|
| ||
| sin∠COB |
|
| ||
| sin∠OCB |
∴|
| b |
| 2 | ||
sin
|
| π |
| 2 |
因此|
| b |
故答案为:4.
点评:本题考查了向量的平行四边形法则、正弦定理、向量的夹角,考查了推理能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
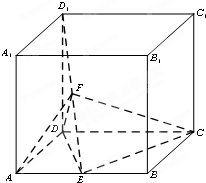 如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.
如图,四棱柱ABCD-A1B1C1D1中,DD1⊥底面ABCD.ABCD为平行四边形,∠DAB=60°,AB=2AD=2.DD1=3,E,F分别是AB与D1E的中点.