题目内容
已知方程cos2x+4sinx-a=0有解，则a的取值范围是 ．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：已知方程利用同角三角函数间基本关系化简表示出a，根据方程有解，利用二次函数的性质即可确定出a的范围．
解答：
解：方程cos2x+4sinx-a=0，
变形得：1-sin2x+4sinx-a=0，即a=-sin2x+4sinx+1=-（sinx-2）2+5，
∵-1≤sinx≤1，
∴-4≤-（sinx-2）2+5≤4，
则a的取值范围为[-4，4]．
故答案为：[-4，4]．
变形得：1-sin2x+4sinx-a=0，即a=-sin2x+4sinx+1=-（sinx-2）2+5，
∵-1≤sinx≤1，
∴-4≤-（sinx-2）2+5≤4，
则a的取值范围为[-4，4]．
故答案为：[-4，4]．
点评：此题考查了的同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
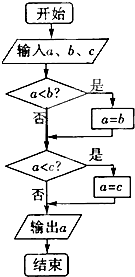阅读如图的算法流程图：若a=sin60°，b=cos60°，c=tan60°，则输出的应该是