题目内容
函数y=sin2x+2cosx-3的最大值是 ．
考点：同角三角函数间的基本关系,二次函数在闭区间上的最值
专题：三角函数的求值
分析：利用同角三角函数的基本关系可得y=-（cosx-1）2-1，结合-1≤cosx≤1并利用二次函数的性质求得函数的最大值．
解答：
解：∵y=-cos2x+2cosx-2=-（cosx-1）2-1，-1≤cosx≤1，
∴当cosx=1时，函数y取得最大值为-1，
故答案为：-1．
∴当cosx=1时，函数y取得最大值为-1，
故答案为：-1．
点评：本题主要考查同角三角函数的基本关系、余弦函数的值域，二次函数的性质的应用，属于基础题．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
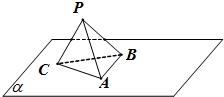已知三棱锥P-ABC的侧面PAC⊥底面ABC，侧棱PA⊥AB，且PA=PC=AC=AB=4．如图AB?平面α，以直线AB为轴旋转三棱锥，记该三棱锥在平面α上的俯视图面积为S，则S的最小值是