题目内容
已知集合M={x|
＜0}，若2∉M，则实数a的取值范围是 ．
| a2x+2x-3 |
| ax-1 |
考点：元素与集合关系的判断
专题：集合
分析：由集合M={x|
＜0}，若2∉M，可得：当x=2时，不等式
＜0无意义，或
≥0，分类求出满足条件的实数a的取值范围，综合讨论结果可得答案．
| a2x+2x-3 |
| ax-1 |
| a2x+2x-3 |
| ax-1 |
| a2x+2x-3 |
| ax-1 |
解答：
解：∵已知集合M={x|
＜0}，若2∉M，
则当x=2时，不等式
＜0无意义，或
≥0，
若x=2时，不等式
＜0无意义，则a=
，
若x=2时，
≥0，则
≥0，解得a＞
，
综上所述，实数a的取值范围是[
，+∞），
故答案为：[
，+∞）
| a2x+2x-3 |
| ax-1 |
则当x=2时，不等式
| a2x+2x-3 |
| ax-1 |
| a2x+2x-3 |
| ax-1 |
若x=2时，不等式
| a2x+2x-3 |
| ax-1 |
| 1 |
| 2 |
若x=2时，
| a2x+2x-3 |
| ax-1 |
| 2a2+1 |
| 2a-1 |
| 1 |
| 2 |
综上所述，实数a的取值范围是[
| 1 |
| 2 |
故答案为：[
| 1 |
| 2 |
点评：本题考查的知识点是元素与集合关系的判断，其中易忽略x=2时，不等式
＜0无意义的情况，造成错解．
| a2x+2x-3 |
| ax-1 |
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
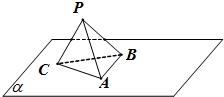已知三棱锥P-ABC的侧面PAC⊥底面ABC，侧棱PA⊥AB，且PA=PC=AC=AB=4．如图AB?平面α，以直线AB为轴旋转三棱锥，记该三棱锥在平面α上的俯视图面积为S，则S的最小值是