题目内容
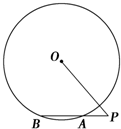如图所示，过点P的直线与⊙O相交于A，B两点．若PA=1，AB=2，PO=3，求⊙O的半径r．考点：与圆有关的比例线段
专题：直线与圆,立体几何
分析：设⊙O的半径为r（r＞0），延长PO交⊙O于点C，PC=PO+r=3+r．设PO交⊙O于点D，PD=3-r．由此利用圆的割线定理能求出⊙O的半径r．
解答：
解：设⊙O的半径为r（r＞0），
∵PA=1，AB=2，∴PB=PA+AB=3．
延长PO交⊙O于点C，
则PC=PO+r=3+r．
设PO交⊙O于点D，
则PD=3-r．
由圆的割线定理知，PA•PB=PD•PC，
∴1×3=（3-r）（3+r），
解得r=
．
∴⊙O的半径r为
．
解：设⊙O的半径为r（r＞0），
∵PA=1，AB=2，∴PB=PA+AB=3．
延长PO交⊙O于点C，
则PC=PO+r=3+r．
设PO交⊙O于点D，
则PD=3-r．
由圆的割线定理知，PA•PB=PD•PC，
∴1×3=（3-r）（3+r），
解得r=
| 6 |
∴⊙O的半径r为
| 6 |
点评：本题考查圆的半径的求法，是中档题，解题时要认真审题，注意圆的割线定理的合理运用．
练习册系列答案
相关题目