题目内容
已知数列{an},a1=2,an=2an-1+2n(n≥2)
(1)求证:{
}为等差数列;
(2)求{an}的前n项和Sn;
(3)若bn=
,求数列{bn}中的最大值.
(1)求证:{
| an |
| 2n |
(2)求{an}的前n项和Sn;
(3)若bn=
| 2n-1 |
| an |
考点:数列的求和,等差关系的确定,数列递推式
专题:计算题,等差数列与等比数列
分析:(1)对an=2an-1+2n(n≥2)两边同除以2n,得
=
+1,整理有
-
=1,由等差数列的定义可作出判断;
(2)由(1)易求an=n•2n,利用错位相减法可求得Sn;
(3)易求bn,bn+1,利用作商可判断bn+1<bn,从而知{bn}为递减数列,进而得到答案;
| an |
| 2n |
| 2an-1 |
| 2n |
| an |
| 2n |
| an-1 |
| 2n-1 |
(2)由(1)易求an=n•2n,利用错位相减法可求得Sn;
(3)易求bn,bn+1,利用作商可判断bn+1<bn,从而知{bn}为递减数列,进而得到答案;
解答:
解:(1)∵a1=2,an=2an-1+2n(n≥2),
∴
=
+1,∴
-
=1,
∴{
}为等差数列,首项为
=1,公差d=1,
(2)由(1)得
=1+(n-1)×1=n,
∴an=n•2n,
∴Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n,
2Sn=1•22+2•23+3•23+…+(n-1)•2n+n•2n+1,
两式相减得:-Sn=21+22+23+…+2n-n•2n+1,
=
-n•2n+1,
∴Sn=2-2n+1+n•2n+1=(n-1)•2n+1+2;
(3)bn=
=
>0,
∴bn+1=
,
∴
=
=
,
又∵2(2n2+n-1)-(2n2+n)=2n2+n-2,
当n≥1时,2n2+n-2>0,
∴2(2n2+n-1)>2n2+n>0,
∴
<1即bn+1<bn,
∴{bn}为递减数列,
数列{bn}中的最大值为b1=0.5.
∴
| an |
| 2n |
| 2an-1 |
| 2n |
| an |
| 2n |
| an-1 |
| 2n-1 |
∴{
| an |
| 2n |
| a1 |
| 2 |
(2)由(1)得
| an |
| 2n |
∴an=n•2n,
∴Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n,
2Sn=1•22+2•23+3•23+…+(n-1)•2n+n•2n+1,
两式相减得:-Sn=21+22+23+…+2n-n•2n+1,
=
| 2(1-2n) |
| 1-2 |
∴Sn=2-2n+1+n•2n+1=(n-1)•2n+1+2;
(3)bn=
| 2n-1 |
| an |
| 2n-1 |
| n•2n |
∴bn+1=
| 2n+1 |
| (n+1)•2n+1 |
∴
| bn+1 |
| bn |
| (2n+1)•n |
| (2n-1)(n+1)•2 |
| 2n2+n |
| 2(2n2+n-1) |
又∵2(2n2+n-1)-(2n2+n)=2n2+n-2,
当n≥1时,2n2+n-2>0,
∴2(2n2+n-1)>2n2+n>0,
∴
| bn+1 |
| bn |
∴{bn}为递减数列,
数列{bn}中的最大值为b1=0.5.
点评:本题考查等差关系的确定、数列求和等知识,考查考查学生的推理论证能力、运算求解能力.

练习册系列答案
相关题目
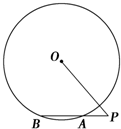 如图所示,过点P的直线与⊙O相交于A,B两点.若PA=1,AB=2,PO=3,求⊙O的半径r.
如图所示,过点P的直线与⊙O相交于A,B两点.若PA=1,AB=2,PO=3,求⊙O的半径r.