题目内容

在极坐标系下，点P（2，
π
2
）到直线ρcos（θ-
π
3
）=2的距离为
 
．
考点：简单曲线的极坐标方程
专题：选作题,坐标系和参数方程
分析：先把点坐标化为直角坐标、极坐标方程化为直角坐标方程，然后利用点到直线的距离公式可得答案．
解答： 解：点P（2，
π
2
）的直角坐标为（0，2），直线ρcos（θ-
π
3
）=2的直角坐标方程为x+
3
y-4=0，
由点到直线的距离公式可得d=
|0+2
3
-4|
2
=2-
3
．
故答案为：2-
3
．
点评：本题考查点的极坐标和直角坐标的互化，考查点到直线的距离公式，属基础题．
练习册系列答案
相关题目
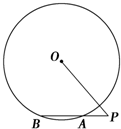如图所示，过点P的直线与⊙O相交于A，B两点．若PA=1，AB=2，PO=3，求⊙O的半径r．
已知集合U={1，2，3，4，5}，A={1，3，5}，B={3，4}，（∁UA）∩B=
 
．
若tan（α+
π
4
）=
3
4
，则tan2α的值是
 
．
∫
π
3
0
（2x+sinx）dx=
 
．
如果K2的观测值为6.645，可以认为“x与y无关”的可信度是
 
．
总体有编号为001，002，…，599，600的600个个体组成．利用下面的随机数表选取60个个体，选取方法是从随机数表第8行第8列的数8开始向右读，则选出来的第5个个体的编号为
 
．（下面摘取了随机数表第7行至第9行）
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 63 01 63 
78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79 33 21 12 34 29 78 
64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54．
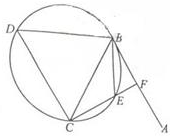如图，直线AB为圆的切线，切点为B，点C在圆上，∠ABC的角平分线BE交圆于点E，DB垂直BE交圆于点D．
（Ⅰ）证明：DB=DC；
（Ⅱ）设圆的半径为1，BC=
3
，延长CE交AB于点F，求△BCF外接圆的半径．
cos22°cos38°-sin22°sin38°的值是（　　）
A、
3
2
B、
1
2
C、-
1
2
D、-
3
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网