题目内容
（1）若a、b、c都是正数，且a+b+c=1，求证：（1-a）（1-b）（1-c）≥8abc．
（2）已知a，b，c都是正数，且a，b，c成等比数列，求证：a2+b2+c2＞（a-b+c）2．
（2）已知a，b，c都是正数，且a，b，c成等比数列，求证：a2+b2+c2＞（a-b+c）2．
考点：不等式的证明,等比数列的性质
专题：证明题,不等式的解法及应用
分析：（1）（1-a）（1-b）（1-c）=（b+c）（ a+c）（ a+b），利用基本不等式，可得结论；
（2）证明b2=ac，a+c＞b，左-右=2（ab+bc-ac），即可得出结论．
（2）证明b2=ac，a+c＞b，左-右=2（ab+bc-ac），即可得出结论．
解答：
证明：（1）∵a、b、c都是正数，且a+b+c=1，
∴（1-a）（1-b）（1-c）=（b+c）（ a+c）（ a+b）≥2
•2
•2
=8abc．
（2）∵a，b，c成等比数列，b2=ac
又∵a，b，c都是正数，∴0＜b=
≤
＜a+c，∴a+c＞b
∴左-右=2（ab+bc-ac）=2（ab+bc-b2）=2b（a+c-b）＞0
∴a2+b2+c2＞（a-b+c）2．
∴（1-a）（1-b）（1-c）=（b+c）（ a+c）（ a+b）≥2
| bc |
| ac |
| ab |
（2）∵a，b，c成等比数列，b2=ac
又∵a，b，c都是正数，∴0＜b=
| ac |
| a+c |
| 2 |
∴左-右=2（ab+bc-ac）=2（ab+bc-b2）=2b（a+c-b）＞0
∴a2+b2+c2＞（a-b+c）2．
点评：本题考查不等式的证明，考查基本不等式的运用，考查作差法，属于中档题．
练习册系列答案
相关题目
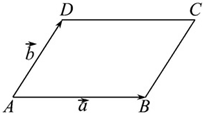如图，?ABCD中，
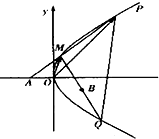已知点A（-1，0），B（1，-1）和抛物线C：y2=4x，O为坐标原点，过点A的动直线l交抛物线C于M、P，直线MB交抛物线C于另一点Q，如图
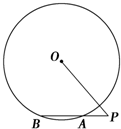如图所示，过点P的直线与⊙O相交于A，B两点．若PA=1，AB=2，PO=3，求⊙O的半径r．