题目内容
已知抛物线x2=2py(p>0)的焦点为F,A,B,C都是抛物线上的点,满足
+
+
=
,则kAB+kBC+kAC=( )
| FA |
| FB |
| FC |
| 0 |
| A、0 | ||
B、
| ||
| C、1 | ||
| D、不能确定 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:设A(x1,y1),B(x2,y2),C(x3,y3),依题意,知F为三角形ABC的重心,于是有
=0,利用“点差法”可求得kAB=
,kBC=
,kAC=
,从而可得答案.
| x1+x2+x3 |
| 3 |
| x1+x2 |
| 2p |
| x2+x3 |
| 2p |
| x1+x3 |
| 2p |
解答:
解:∵抛物线x2=2py(p>0)的焦点F(0,
),
设A(x1,y1),B(x2,y2),C(x3,y3),因向量
+
+
=
,则F为三角形ABC的重心.
故
=0,
=
,
又x12=2py1,x22=2py2,
两式相减,得:(x1+x2)(x1-x2)=2p(y1-y2),
所以,kAB=
=
;
同理可得,kBC=
,kAC=
,
所以,kAB+kBC+kAC=
=0,
故选:A.
| p |
| 2 |
设A(x1,y1),B(x2,y2),C(x3,y3),因向量
| FA |
| FB |
| FC |
| 0 |
故
| x1+x2+x3 |
| 3 |
| y1+y2+y3 |
| 3 |
| p |
| 2 |
又x12=2py1,x22=2py2,
两式相减,得:(x1+x2)(x1-x2)=2p(y1-y2),
所以,kAB=
| y2-y1 |
| x2-x1 |
| x1+x2 |
| 2p |
同理可得,kBC=
| x2+x3 |
| 2p |
| x1+x3 |
| 2p |
所以,kAB+kBC+kAC=
| 2(x1+x2+x3) |
| 2p |
故选:A.
点评:本题考查抛物线的标准方程与简单几何性质,考查“点差法”与三角形的“重心”的坐标表示,求得kAB=
=
是关键,是好题.
| y2-y1 |
| x2-x1 |
| x1+x2 |
| 2p |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )
如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
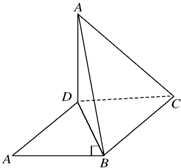 如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )
如图,平行四边形ABCD中,AB⊥BD,沿BD将△ABD折起到A′BD,使面A′BD⊥面BCD,连接A′C,则在四面体A′BCD的四个面中,互相垂直的平面有( )①面ABD⊥面BCD;
②面A′CD⊥面ABD;
③面A′BC⊥面BCD;
④面ACD⊥面ABC.
| A、1个 | B、2个 | C、3个 | D、4个 |
设a、b∈z,且a≠0,则(a-b)a2<0,且a<b的( )条件.
| A、充分不必要 |
| B、必要而不充分 |
| C、充要 |
| D、既不充分也不必要 |
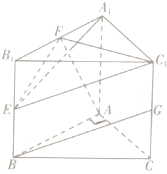 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.
已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.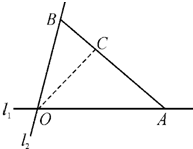 如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(
如图,在C城周边已有两条公路l1,l2在点O处交汇,且它们的夹角为75°.已知OC=(