题目内容
已知直线l:y=x+m(m∈R)与直线l′关于x轴对称.
(1)若直线l与圆(x-2)2+y2=8相切于点P,求m的值和P点的坐标;
(2)直线l′过抛物线C:x2=4y的焦点,且与抛物线C交于A,B两点,求|AB|的值.
(1)若直线l与圆(x-2)2+y2=8相切于点P,求m的值和P点的坐标;
(2)直线l′过抛物线C:x2=4y的焦点,且与抛物线C交于A,B两点,求|AB|的值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)因为直线l与圆(x-2)2+y2=8相切于点P,点P到直线的距离等于半径,由点到直线的距离公式求得m的值,再代入求得P的坐标;
(Ⅱ)先根据对称和过抛物线C:x2=4y的焦点求出直线l′,再根据韦达定理求得y1+y2=-4(x1+x2)+2=6,再根据焦半径求出|AB|的长.
(Ⅱ)先根据对称和过抛物线C:x2=4y的焦点求出直线l′,再根据韦达定理求得y1+y2=-4(x1+x2)+2=6,再根据焦半径求出|AB|的长.
解答:
解:(Ⅰ)由点到直线的距离公式:d=
=2
,
解得m=2,或m=-6,
当m=2时,P的坐标为(0,2),
当m=-6时,P的坐标为(4,-2),
(Ⅱ)∵直线l:y=x+m(m∈R),
∴直线l′的方程为y=-x-m,
∵抛物线C:x2=4y
∴焦点坐标(0,1),
∴m=-1,
设A,B两点坐标为(x1,y1),(x2,y2)
将直线y=-x+1代入抛物线x2=4y,整理得x2+4x-4=0,
∴x1+x2=-4,
∴y1+y2=-4(x1+x2)+2=6,
∴|AB|=y1+y2+2=8
| |2+m| | ||
|
| 2 |
解得m=2,或m=-6,
当m=2时,P的坐标为(0,2),
当m=-6时,P的坐标为(4,-2),
(Ⅱ)∵直线l:y=x+m(m∈R),
∴直线l′的方程为y=-x-m,
∵抛物线C:x2=4y
∴焦点坐标(0,1),
∴m=-1,
设A,B两点坐标为(x1,y1),(x2,y2)
将直线y=-x+1代入抛物线x2=4y,整理得x2+4x-4=0,
∴x1+x2=-4,
∴y1+y2=-4(x1+x2)+2=6,
∴|AB|=y1+y2+2=8
点评:本题考查了直线和圆的位置关系,以及弦的长度,培养了学生的计算能力,属于中档题

练习册系列答案
相关题目
已知函数f(x)=|x2+3x|,x∈R,若函数y=f(x)-a|x-1|恰有4个零点,则实数a的取值范围为( )
| A、(0,1)∪[9,+∞) |
| B、(0,1)∪(9,+∞) |
| C、(1,9] |
| D、(1,9) |
 如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )
如图,已知F1、F2为椭圆的焦点,等边三角形AF1F2两边的中点M,N在椭圆上,则椭圆的离心率为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知PA垂直于正方形ABCD所在的平面,若PA=2,AB=4,求:
已知PA垂直于正方形ABCD所在的平面,若PA=2,AB=4,求: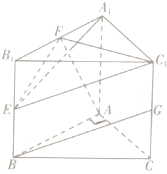 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.
已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.