题目内容
已知函数f(x)=
(1)判断该函数的奇偶性;
(2)判断该函数的单调性,不必证明;
(3)求该函数的值域.
| 2x-2-x |
| 2x+2-x |
(1)判断该函数的奇偶性;
(2)判断该函数的单调性,不必证明;
(3)求该函数的值域.
考点:函数奇偶性的判断,函数的值域,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)根据函数奇偶性的定义即可判断函数f(x)的奇偶性.
(2)根据指数函数的性质即可求函数f(x)的单调性
(3)根据指数函数性质即可求值域.
(2)根据指数函数的性质即可求函数f(x)的单调性
(3)根据指数函数性质即可求值域.
解答:
解:(1)函数的定义域为R,
则f(-x)=
=-
=-f(x),
即函数f(x)为奇函数.
(2)原函数化为:f(x)=
在(-∞,+∞)是一个增函数.
f(x)=
=
=1-
,
在(-∞,+∞)上,4x+1递增且函数值大于0,
在(-∞,+∞)上是减函数,
故f(x)=1-
,在(-∞,+∞)上是增函数.
(3)∵原函数化为:f(x)=
,
函数的解析式可以变为f(x)=
=
=1-
,
由于4x+1>1,故0<
<1
故0<
<2,
-1<1-
<1
∴f(x)的值域是(-1,1)
f(x)=
=1-
,
∵y=2x为增函数,∴y=2x+1为增函数,
则f(x)=
=1-
为增函数,
由y=f(x)=
得(1-y)2x=1+y,
当y=1时,不成立,则方程等价为2x=
,
由2x=
>0,解得-1<y<1,
故函数的值域为(-1,1).
则f(-x)=
| 2-x-2x |
| 2-x+2x |
| 2x-2-x |
| 2x+2-x |
即函数f(x)为奇函数.
(2)原函数化为:f(x)=
| 4x-1 |
| 4x+1 |
f(x)=
| 4x-1 |
| 4x+1 |
| 4x+1-2 |
| 4x+1 |
| 2 |
| 4x+1 |
在(-∞,+∞)上,4x+1递增且函数值大于0,
| 2 |
| 4x+1 |
故f(x)=1-
| 2 |
| 4x+1 |
(3)∵原函数化为:f(x)=
| 4x-1 |
| 4x+1 |
函数的解析式可以变为f(x)=
| 4x-1 |
| 4x+1 |
| 4x+1-2 |
| 4x+1 |
| 2 |
| 4x+1 |
由于4x+1>1,故0<
| 1 |
| 4x+1 |
故0<
| 2 |
| 4x+1 |
-1<1-
| 2 |
| 4x+1 |
∴f(x)的值域是(-1,1)
f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
∵y=2x为增函数,∴y=2x+1为增函数,
则f(x)=
| 2x-1 |
| 2x+1 |
| 2 |
| 2x+1 |
由y=f(x)=
| 2x-1 |
| 2x+1 |
当y=1时,不成立,则方程等价为2x=
| 1+y |
| 1-y |
由2x=
| 1+y |
| 1-y |
故函数的值域为(-1,1).
点评:本题考查函数单调性的、奇偶性的判断与证明以及函数的值域的求法,求解此类题的关键是对函数性质的证明方法熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知集合P=﹛0,1﹜,Q=﹛0,1,2﹜,则P∩Q=( )
| A、{0} | B、{0,1} |
| C、{1} | D、{0,1,2}. |
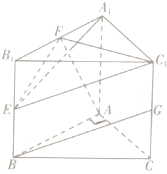 已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.
已知三棱柱ABC-A1B1C1中,AA1⊥底面ABC,AA1=AC=AB,∠BAC=90°,点E,F,G分别是棱BB1,A1B1,CC1的中点.求证:AF⊥BG.