题目内容
已知(x+
)n展开式的二项式系数之和为256.
(1)求n;
(2)若展开式中常数项为
,求m的值;
(3)若(x+m)n展开式中系数最大项只有第6项和第7项,求m的取值情况.
| m |
| x |
(1)求n;
(2)若展开式中常数项为
| 35 |
| 8 |
(3)若(x+m)n展开式中系数最大项只有第6项和第7项,求m的取值情况.
考点:二项式系数的性质
专题:二项式定理
分析:(1)根据二项式系数之和为2n=256,可得n的值.
(2)二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项,再根据常数项为
,求得m的值.
(3)易知m>0,设第r+1项系数最大.则
,化简,根据只有第6项和第7项系数最大,求得m的值.
(2)二项式展开式的通项公式,再令x的幂指数等于0,求得r的值,即可求得展开式中的常数项,再根据常数项为
| 35 |
| 8 |
(3)易知m>0,设第r+1项系数最大.则
|
解答:
解:(1)二项式系数之和为2n=256,可得n=8.
(2)设常数项为第r+1项,则Tr+1=
x8-r(
)r=
mrx8-2r,
故8-2r=0,即r=4,
则
m4=
,解得m=±
.
(3)易知m>0,设第r+1项系数最大.
则
化简可得
≤r≤
.
由于只有第6项和第7项系数最大,
所以
,即
,
所以m只能等于2.
(2)设常数项为第r+1项,则Tr+1=
| C | r 8 |
| m |
| x |
| C | r 8 |
故8-2r=0,即r=4,
则
| C | 4 8 |
| 35 |
| 8 |
| 1 |
| 2 |
(3)易知m>0,设第r+1项系数最大.
则
|
| 8m-1 |
| m+1 |
| 9m |
| m+1 |
由于只有第6项和第7项系数最大,
所以
|
|
所以m只能等于2.
点评:本题主要考查二项式定理的应用,二项式系数的性质,二项式展开式的通项公式,求展开式中某项的系数,属于基础题.

练习册系列答案
相关题目
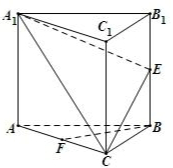 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
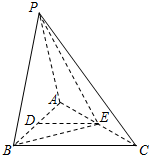 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.