题目内容
若对任意a,b,c∈R+,且a2+b2+c2=1,求证:a+b+
c≤2.
| 2 |
考点:综合法与分析法(选修)
专题:不等式的解法及应用
分析:利用分析法证明不等式,对不等式两边平方,通过已知条件以及基本不等式证明即可.
解答:
解:原不等式等价于(a+b+
c)2≤4…(2分)
即证a2+b2+2c2+2ab+2
ac+2
bc≤4…(4分)
即证c2+2ab+2
ac+2
bc≤3…(6分)
又c2+2ab+2
ac+2
bc≤c2+a2+b2+(
a)2+(
b)2+c2=3成立,
当且仅当a=b=
时,等号成立.…(11分)
所以a+b+
c≤2…(12分)
| 2 |
即证a2+b2+2c2+2ab+2
| 2 |
| 2 |
即证c2+2ab+2
| 2 |
| 2 |
又c2+2ab+2
| 2 |
| 2 |
| 2 |
| 2 |
当且仅当a=b=
| c | ||
|
所以a+b+
| 2 |
点评:本题考查不等式的证明,分析法证明方法的应用,考查分析问题解决问题的能力.

练习册系列答案
相关题目
在△ABC中,已知tanA•tanB>1,则△ABC是( )
| A、直角三角形 |
| B、钝角三角形 |
| C、锐角三角形 |
| D、最小内角大于45°的三角形 |
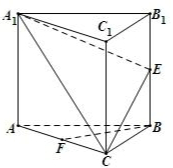 如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.
如图,在正三棱柱ABC-A1B1C1中,E,F分别为BB1,AC的中点.