题目内容
6.(1)已知双曲线的中心在原点,焦点在坐标轴上,焦距为6,离心率为3,求双曲线的标准方程;(2)已知抛物线的顶点在原点,对称轴是x轴,且焦点到准线的距离为1,求抛物线的标准方程.
分析 (1)利用已知条件求解双曲线方程即可,注意两种形式.
(2)利用抛物线的性质,真假写出抛物线方程即可.
解答 解:(1)双曲线的中心在原点,焦点在坐标轴上,焦距为6,离心率为3,可得:c=3,a=1,则b=2$\sqrt{2}$,
所求的双曲线方程为:${x^2}-\frac{y^2}{8}=1或{y^2}-\frac{x^2}{8}=1$.
(2)抛物线的顶点在原点,对称轴是x轴,且焦点到准线的距离为1,
可得p=1,所求抛物线方程为:y2=2x或y2=-2x
点评 本题考查抛物线以及双曲线的简单性质的应用,双曲线方程以及抛物线方程的求法,考查计算能力.

练习册系列答案
相关题目
16.若函数$f(x)=\frac{2}{3}{x^3}-2{x^2}+ax+10$在区间[-1,4]上单调递减,则实数a的取值范围是( )
| A. | (-∞,-16]∪[2,+∞) | B. | (-16,2) | C. | [2,+∞) | D. | (-∞,-16] |
14.已知函数f(x)对任意的x,y∈R都有f(x+y)=f(x)+f(y),且f(2)=4,则f(1)=( )
| A. | -2 | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
18.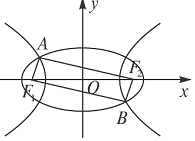 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
 如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )
如图,F1,F2是椭圆${C_1}:\frac{x^2}{4}+{y^2}=1$与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则双曲线C2的渐近线方程是( )| A. | $y=±\sqrt{2}x$ | B. | $y=±\frac{{\sqrt{2}}}{2}x$ | C. | y=±$\sqrt{3}$x | D. | y=±$\frac{{\sqrt{6}}}{2}$x |
16.心理学家分析发现“喜欢空间想象”与“性别”有关,某数学兴趣小组为了验证此结论,从全球组员中按分层抽样的方法抽取50名同学(男生30人、女生20人),给每位同学立体几何题,代数题各一道,让各位同学自由选择一道题进行解答,选题情况统计如表:(单位:人)
(Ⅰ)能否有97.5%以上的把握认为“喜欢空间想象”与“性别”有关?
(Ⅱ)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行探究,记抽取的两人中答对的人数为X,求 X的分布列及数学期望.
附表及公式
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$.
| 立体几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
(Ⅱ)经统计得,选择做立体几何题的学生正答率为$\frac{4}{5}$,且答对的学生中男生人数是女生人数的5倍,现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行探究,记抽取的两人中答对的人数为X,求 X的分布列及数学期望.
附表及公式
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |