题目内容
(1)已知x>0、y>0,且
+
=1,求x+y的最小值.
(2)设a、b、c>0,证明:
+
+
≥a+b+c.
| 1 |
| x |
| 9 |
| y |
(2)设a、b、c>0,证明:
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
考点:不等式的证明
专题:综合题,不等式的解法及应用
分析:(1)利用“乘1法”和基本不等式的性质即可得出.
(2)利用基本不等式,即可证明结论.
(2)利用基本不等式,即可证明结论.
解答:
(1)解:∵x>0、y>0,且
+
=1,
∴x+y=(x+y)(
+
)=
+
+10≥6+10=16.
当且仅当
=
时,上式等号成立,又
+
=1,
可得x=4,y=12时,(x+y)min=16.
(2)证明:∵a、b、c>0,
∴
+b≥2a,
+c≥2b,
+a≥2c,
∴
+b+
+c+
+a≥2a+2b+2c,
∴
+
+
≥a+b+c.
| 1 |
| x |
| 9 |
| y |
∴x+y=(x+y)(
| 1 |
| x |
| 9 |
| y |
| y |
| x |
| 9x |
| y |
当且仅当
| y |
| x |
| 9x |
| y |
| 1 |
| x |
| 9 |
| y |
可得x=4,y=12时,(x+y)min=16.
(2)证明:∵a、b、c>0,
∴
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
∴
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
∴
| a2 |
| b |
| b2 |
| c |
| c2 |
| a |
点评:本题考查了“乘1法”和基本不等式的性质,考查基本不等式的运用,属于中档题.

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
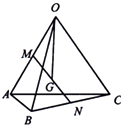 已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设
已知空间四边形OABC,M,N分别是OA,BC的中点,点G是线段MN的中点,设| OG |
| OA |
| OB |
| OC |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|