题目内容
设F1,F2是椭圆E:
+
=1,(a>b>0)得左右焦点,过F1斜率为1的直线l与E交于A,B两点,且|AF2|,|AB|,|BF2|成等差数列.
(1)求E的离心率;
(2)设点P(0,-1)满足|PA|=|PB|,求E的方程.
| x2 |
| a2 |
| y2 |
| b2 |
(1)求E的离心率;
(2)设点P(0,-1)满足|PA|=|PB|,求E的方程.
考点:轨迹方程,椭圆的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)根据|AF2|,|AB|,|BF2|成等差数列,可得2|AB|=|AF2|+|BF2|,利用椭圆定义可得|AB|=
a.设l:x=y-c,代入椭圆C的方程,整理得(a2+b2)y2-2b2cy-b4=0(*),利用韦达定理可得
a,从而可求E的离心率.
(2)由(1)有b=c,方程(*)可化为3y2-2by-b2=0,根据|PA|=|PB|知PM为AB的中垂线,可得kPM=-1,从而可求b=3,进而可求椭圆C的方程.
| 4 |
| 3 |
| 4 |
| 3 |
(2)由(1)有b=c,方程(*)可化为3y2-2by-b2=0,根据|PA|=|PB|知PM为AB的中垂线,可得kPM=-1,从而可求b=3,进而可求椭圆C的方程.
解答:
解:(1)∵|AF2|,|AB|,|BF2|成等差数列,
∴2|AB|=|AF2|+|BF2|,
由椭圆定义|AB|+|AF2|+|BF2|=4a,
所以,|AB|=
a.
设A(x1,y1),B(x2,y2),F1(-c,0),l:x=y-c,
代入椭圆C的方程,整理得(a2+b2)y2-2b2cy-b4=0,(*)
则|AB|2=(x1-x2)2+(y1-y2)2=2(y1-y2)2=2[(y1+y2)2-4y1y2]
=2[(
)2+
]=
,
于是有
a=
,化简得a=
b,故e=
.
(2)由(1)有b=c,方程(*)可化为3y2-2by-b2=0,
设AB中点为M(x0,y0),则y0=
(y1+y2)=
,
又M∈l,于是x0=y0-c=-
,
由|PA|=|PB|,知PM为AB的中垂线,kPM=-1,
由P(0,-1),得-1=
,解得b=3,a2=18,
故椭圆C的方程为
+
=1.
∴2|AB|=|AF2|+|BF2|,
由椭圆定义|AB|+|AF2|+|BF2|=4a,
所以,|AB|=
| 4 |
| 3 |
设A(x1,y1),B(x2,y2),F1(-c,0),l:x=y-c,
代入椭圆C的方程,整理得(a2+b2)y2-2b2cy-b4=0,(*)
则|AB|2=(x1-x2)2+(y1-y2)2=2(y1-y2)2=2[(y1+y2)2-4y1y2]
=2[(
| 2b2c |
| a2+b2 |
| 4b2 |
| a2+b2 |
| 16a2b4 |
| (a2+b2)2 |
于是有
| 4 |
| 3 |
| 4ab2 |
| a2+b2 |
| 2 |
| ||
| 2 |
(2)由(1)有b=c,方程(*)可化为3y2-2by-b2=0,
设AB中点为M(x0,y0),则y0=
| 1 |
| 2 |
| b |
| 3 |
又M∈l,于是x0=y0-c=-
| 2b |
| 3 |
由|PA|=|PB|,知PM为AB的中垂线,kPM=-1,
由P(0,-1),得-1=
| ||
-
|
故椭圆C的方程为
| x2 |
| 18 |
| y2 |
| 9 |
点评:本题重点考查椭圆的标准方程,考查等差数列的性质,考查两点间的距离公式,解题的关键是利用PM为AB的中垂线,求得斜率为-1.

练习册系列答案
相关题目
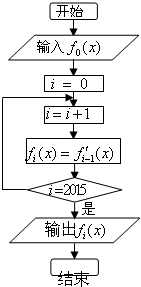
在如图所示的程序框图中,若f0(x)=xex,则输出的结果是( )

| A、2016ex+xex |
| B、2015ex+xex |
| C、2014ex+xex |
| D、2013ex+x |
若点(m,1)在不等式2x+3y-5>0所表示的平面区域内,则m的取值范围是( )
| A、m≥1 | B、m≤1 |
| C、m>1 | D、m<1 |
